Advanced Machine Learning
25: word embedding
background source based on the movie Arrival together with other illustrations to this lecture
Outline of this lecture
- Introduction
- Bag of Words
- Singular Value Decomposition
- Word2vec
Why represent data as vectors?

Vector components may have semantic meanings!
What does a word mean?
let's ask humans
- William Labov. 1973
- Employ human subjects and ask them to label objects on the right as either a bowl or a cup.
- Construct a definition based on their responses.

Labov, W., 1973. The boundaries of words and their meanings. New ways of analyzing variation in English.
based on Daniel Jurafsky's slides
Labov, W., 1973. The boundaries of words and their meanings. New ways of analyzing variation in English.
A definition of "cup" emerges:
Labov, W., 1973. The boundaries of words and their meanings. New ways of analyzing variation in English.
Ludwig Wittgenstein (1889-1951)
- Philosopher of Language
- In his late years, a proponent of studying “ordinary language”
-
In his view if we misuse words, when they have lost their meaning, it could create an inconsistency.
A man loses his dog, so he puts an ad in the paper. And the ad says, ‘Here, boy!’

What is a game?
Wittgenstein "Philosophical Investigations" (1945)
66. Consider for example the proceedings that we call "games". I mean board-games, card-games, ball-games, Olympic games, and so on. What is common to them all? -- Don't say: "There must be something common, or they would not be called 'games' "-but look and see whether there is anything common to all. -- For if you look at them you will not see something that is common to all, but similarities, relationships, and a whole series of them at that. To repeat: don't think, but look! -- Look for example at board-games, with their multifarious relationships. Now pass to card-games; here you find many correspondences with the first group, but many common features drop out, and others appear. When we pass next to ball-games, much that is common is retained, but much is lost. -- Are they all 'amusing'? Compare chess with noughts and crosses. Or is there always winning and losing, or competition between players? Think of patience. In ball games there is winning and losing; but when a child throws his ball at the wall and catches it again, this feature has disappeared. Look at the parts played by skill and luck; and at the difference between skill in chess and skill in tennis. Think now of games like ring-a-ring-a-roses; here is the element of amusement, but how many other characteristic features have disappeared! And we can go through the many, many other groups of games in the same way; can see how similarities crop up and disappear.
And the result of this examination is: we see a complicated network of similarities overlapping and criss-crossing: sometimes overall similarities.
67. I can think of no better expression to characterize these similarities than "family resemblances"; for the various resemblances between members of a family: build, features, colour of eyes, gait, temperament, etc. etc. overlap and criss-cross in the same way.-And I shall say: 'games' form a family.
And for instance the kinds of number form a family in the same way. Why do we call something a "number"? Well, perhaps because it has a-direct-relationship with several things that have hitherto been called number; and this can be said to give it an indirect relationship to other things we call the same name. And we extend our concept of number as in spinning a thread we twist fibre on fibre. And the strength of the thread does not reside in the fact that some on e fibre runs through its whole length, but in the overlapping of many fibres.
But if someone wished to say: "There is something common to all these constructions-namely the disjunction of all their common properties" --I should reply: Now you are only playing with words. One might as well say: "Something runs through the whole thread- namely the continuous overlapping of those fibres".
How about a radically different approach?
"The meaning of a word is its use in the language."
Ludwig Wittgenstein
Words are defined by their environments
the words around them
"If A and B have almost identical environments we say that they are synonyms."
Zellig Harris (1954)
What does 'ong choi' mean?
Suppose you see these sentences:
- Ong choi is delicious sautéed with garlic.
- Ong choi is superb over rice.
- Ong choi leaves with salty sauces
And you've also seen these:
- ...spinach sautéed with garlic over rice
- Chard stems and leaves are delicious
- Collard greens and other salty leafy greens
Conclusion:Ong choi is a leafy green like spinach, chard, or collard greens
Ong choi: Ipomoea aquatica "Water Spinach"
Let's consider methods that embed words in a vector space
Bag of Words
check this for ideas and inspirations https://towardsdatascience.com/art-of-vector-representation-of-words-5e85c59fee5One hot encoding

Simple counts
tfidf
- $$ w_{i,j} = tf_{i,j} $$ $tf_{i,j}$ - term frequency: number of occurrences of word $i$ in $j$
- \begin{align} idf & = - \log{\prob{P}{w_i|D}}\\ & = \log{\frac{1}{\prob{P}{w_i|D}}}\\ & = \log{\left(\frac{N}{df_i}\right)} \end{align} $df_i$ - number of documents containing $i$ $N$ - total number of documents
- $$ w_{i,j} = tf_{i,j} \times \log{\left(\frac{N}{df_i}\right)} $$
n-grams
Take Away Bits
- To use ML models need to vectorize categorical variables
- One-hot encoding (aka 1-in-K) is a good start
- To encode a collection use counts or tf-idf
- To enrich representation use n-grams (beware of the exponent)
Matrix Factorization Method
CO-occurence tables
Fill the table with tfidf instead
- $$ w_{i,j} = tf_{i,j} $$ $tf_{i,j}$ - term frequency: number of occurrences of word $i$ in $j$
- \begin{align} idf & = - \log{\prob{P}{w_i|D}}\\ & = \log{\frac{1}{\prob{P}{w_i|D}}}\\ & = \log{\left(\frac{N}{df_i}\right)} \end{align} $df_i$ - number of documents containing $i$ $N$ - total number of documents
- $$ w_{i,j} = tf_{i,j} \times \log{\left(\frac{N}{df_i}\right)} $$
or use PMI
Pointwise Mutual Information (PMI)
Do words x and y co-occur more than if they were independent? $$ \prob{PMI}{w, c} = \log{\frac{\prob{p}{c,w}}{\prob{p}{w}\prob{p}{c}}} $$
- $$ \prob{PMI}{w, c} = \log{\frac{\prob{p}{c|w}}{\prob{p}{c}}} $$
- $$ \prob{p}{c} = \frac{\prob{count}{c}}{N} $$
- $$ \prob{p}{c|w} = \frac{\prob{p}{c,w}}{\prob{p}{w}} $$
- $$ \prob{p}{c,w} = \frac{\prob{count}{c,w}}{N} $$
- $$ \prob{p}{w} = \frac{\prob{count}{w}}{N} $$
- $$ \log{\frac{\prob{count}{c,w}\times N}{\prob{count}{c}\times \prob{count}{w}}} $$
Positive Pointwise Mutual Information
- PMI ranges from $-\infty$ to $+\infty$
-
But the negative values are problematic
- Things are co-occurring less than we expect by chance
- Unreliable without enormous corpora
- Imagine $w_1$ and $w_2$ whose probability is each $10^{-6}$
- Hard to be sure $\prob{p}{w_1,w_2}$ is significantly different than $10^{-12}$
- It’s not clear people are good at "unrelatedness"
-
Let's try a hack: replace negative PMI values by 0
$$
\prob{PPMI}{w, c} = \begin{cases}
\prob{PMI}{w, c} & \prob{PMI}{w, c} \gt 0 \\
0 & \mbox{otherwise}
\end{cases}
$$
-
PMI is biased toward infrequent events
- Very rare words have very high PMI values
-
Two solutions:
- Give rare words slightly higher probabilities
- Use add-one smoothing (which has a similar effect)
Probability Ratios
Latent Semantic Analysis
Matrix factorization for dense word vectors
SVD for dense word vectors
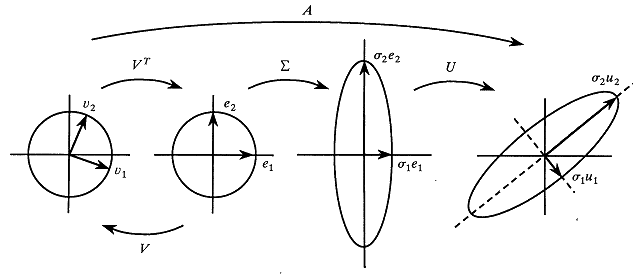
Take Away bits
- Word similarity as co-occurrence within same context.
- Different way to estimate it but all can be put in a matrix.
- The matrix can be low rank factored and dense word representations emerge.
- Inner product of word vectors encodes co-occurrence or probability.
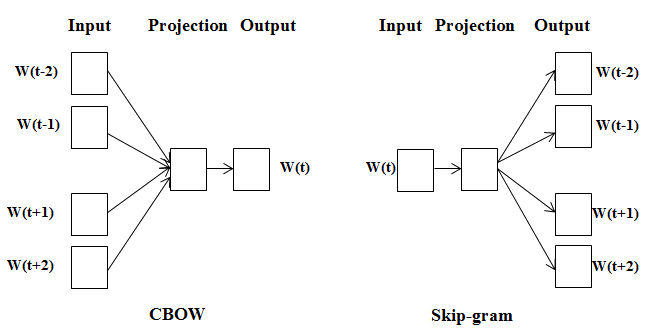
Word2vec
dense embedding with word2vec
w2v: semantic algebra
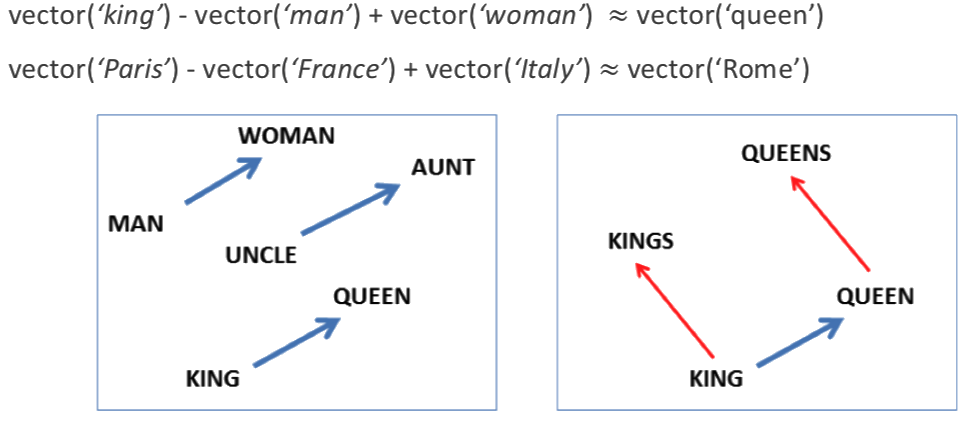
w2v: relation
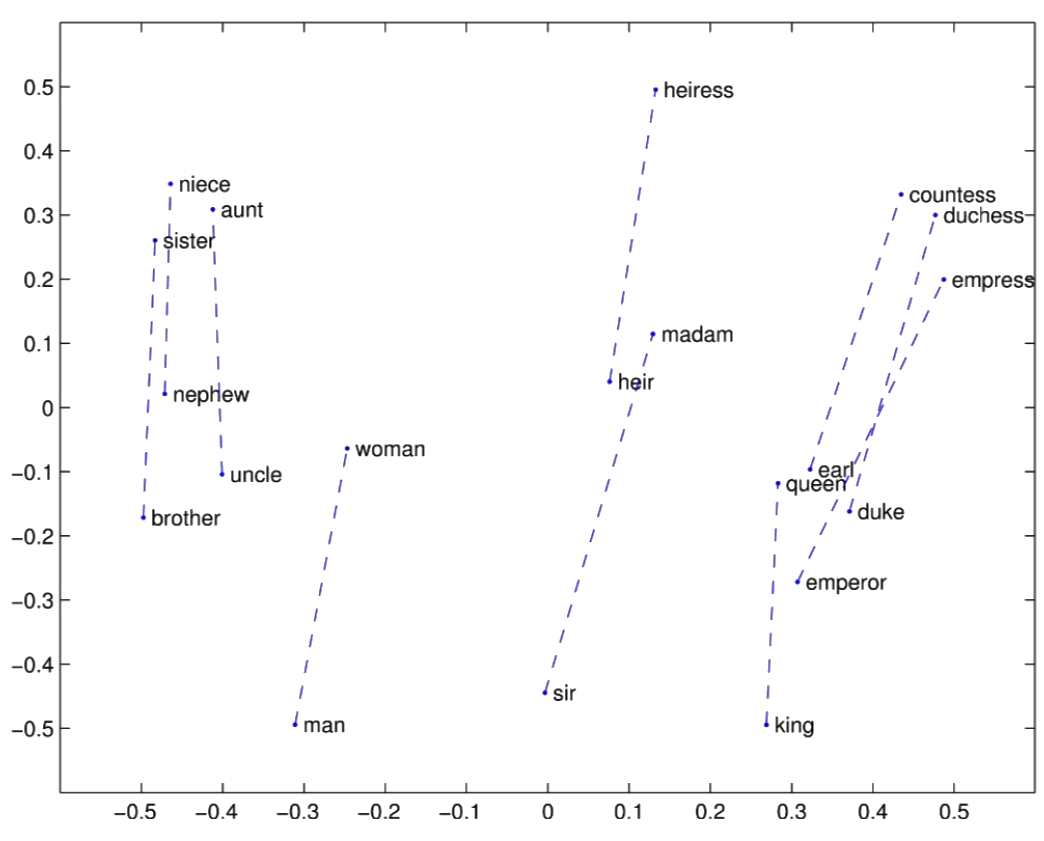
w2v: degree
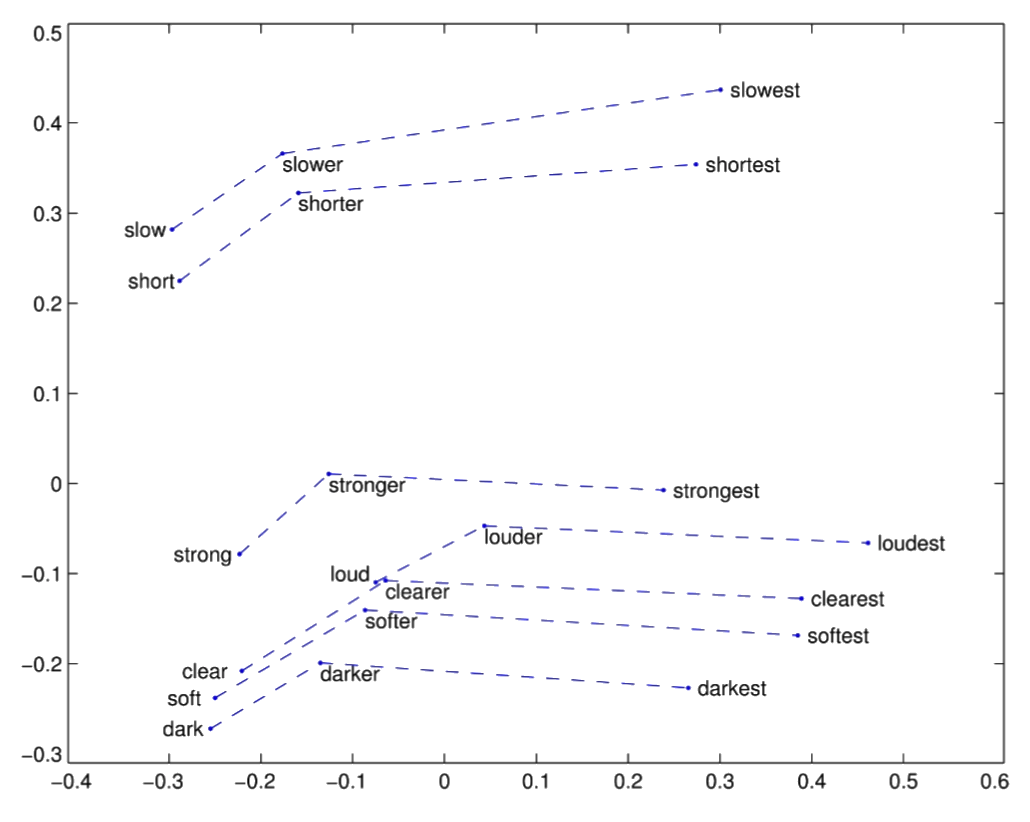
w2v: semantic drift
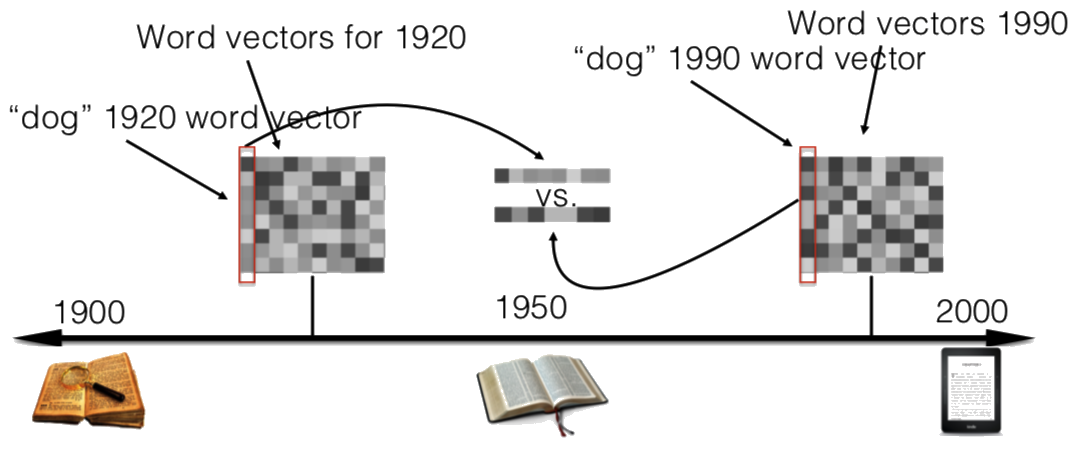
w2v: semantic drift
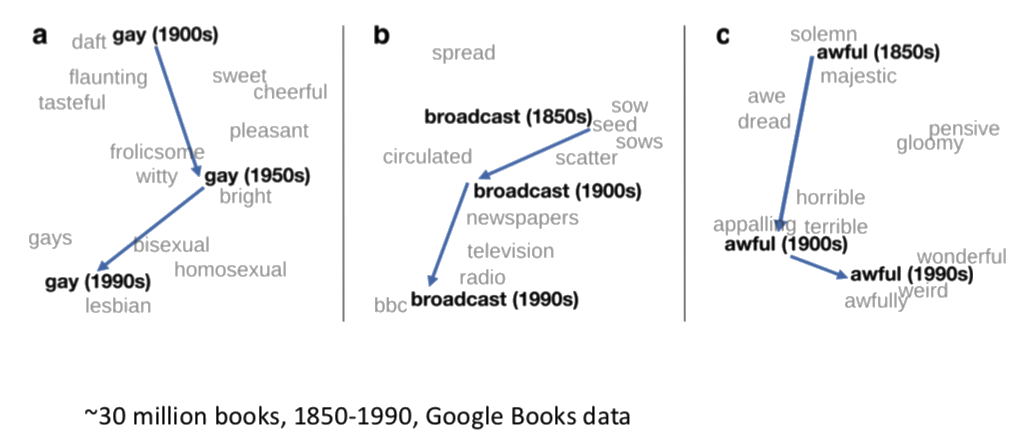
Take Away bits
- Simple and efficient dense word embedding
- Use SGNS unless you know what you're doing
-
But mind this recent result on CBOW: kōan: A Corrected CBOW Implementation
- W2v give semantically rich space (even algebra works)
- If you're encoding words as BOW in your project you're missing out!


