Advanced Machine Learning
24: Convolutional Neural Networks
Outline for the lecture
- History of CNNs
- Bulding Blocks
- Skip Connections
- Fully Convolutional Neural Nets
- Semantic Segmentation with Twists
- (even more) Advanced Uses of CNN
Convolutions what?
History of CNNs
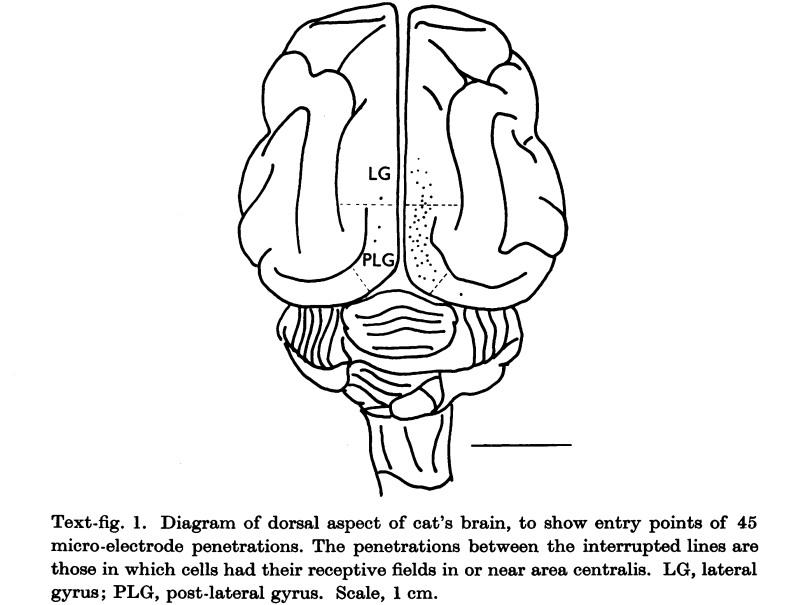
Cat's brain 1962 (Hubel and Wiesel)

Fukushima's Neurocognitron 1979
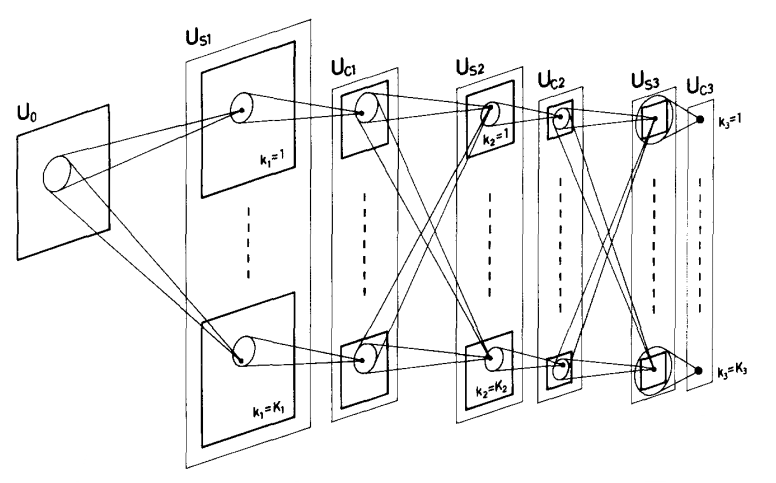

Time Delay Neural Network 1989
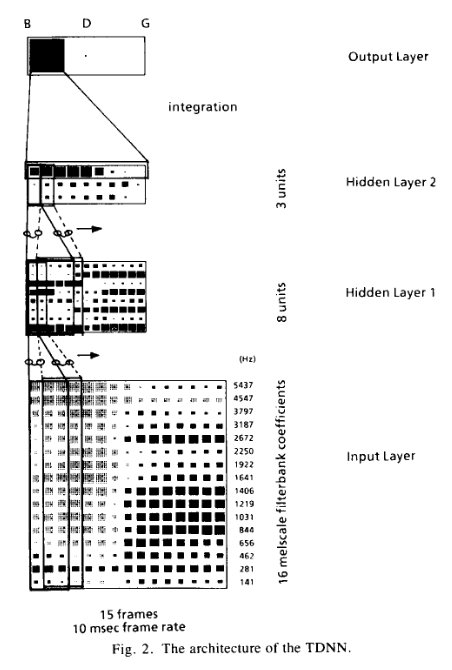

CNN 1989
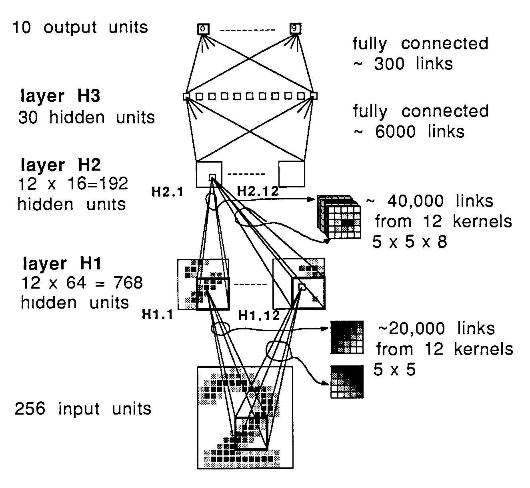

CNN 1998
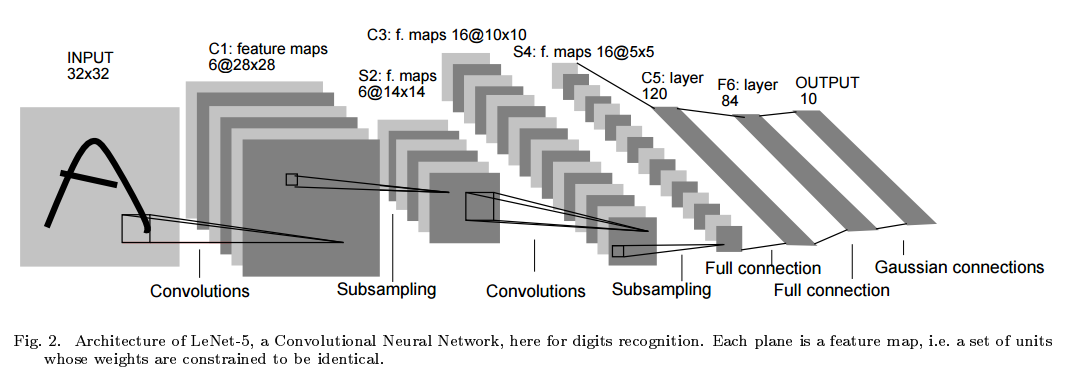

CNN+GPU+MaxPooling 2011

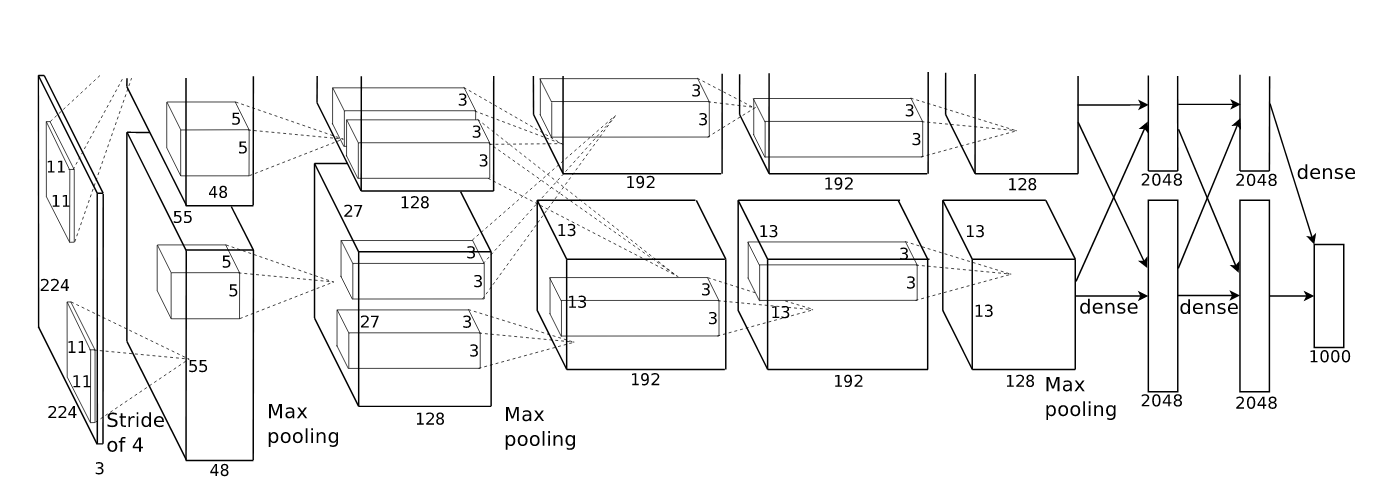
AlexNet 2012
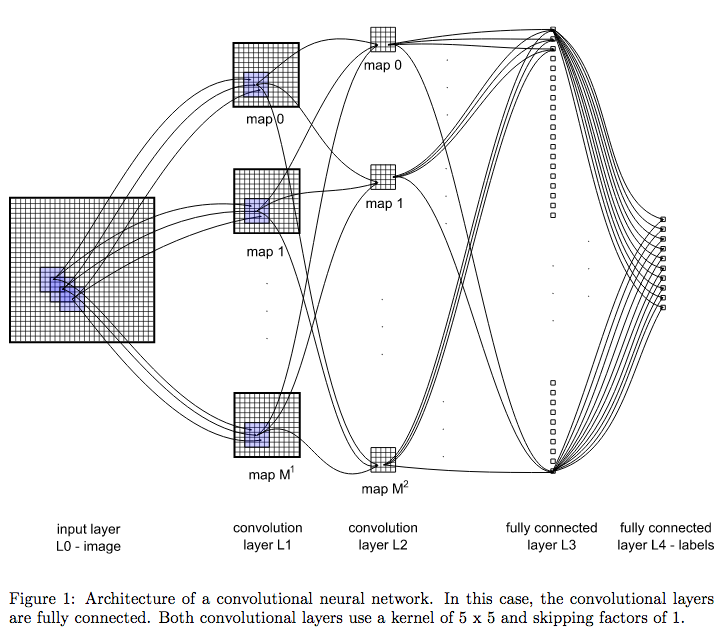
CNN: bulding blocks
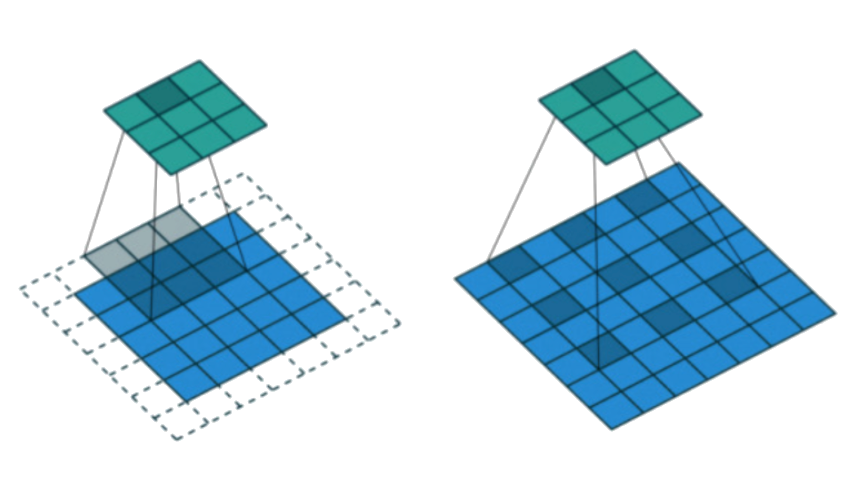
Convolving a kernel with an image
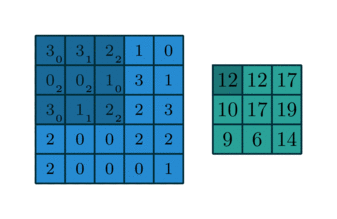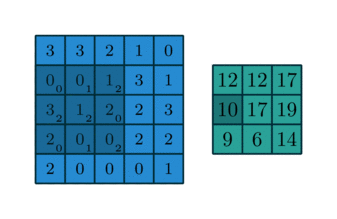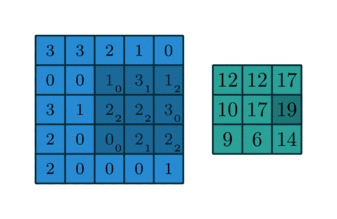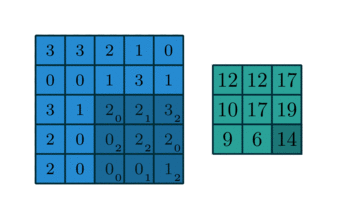 \[
\left(
\begin{array}{ccc}
0 & 1 & 2 \\
2 & 2 & 0 \\
0 & 1 & 2 \\
\end{array}
\right)
\]
\[
\left(
\begin{array}{ccc}
0 & 1 & 2 \\
2 & 2 & 0 \\
0 & 1 & 2 \\
\end{array}
\right)
\]

Convolving a kernel with an image
Padding and symmetries
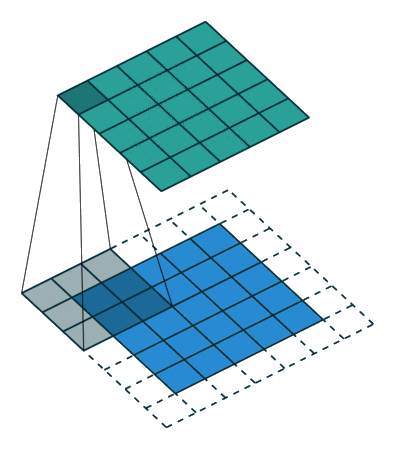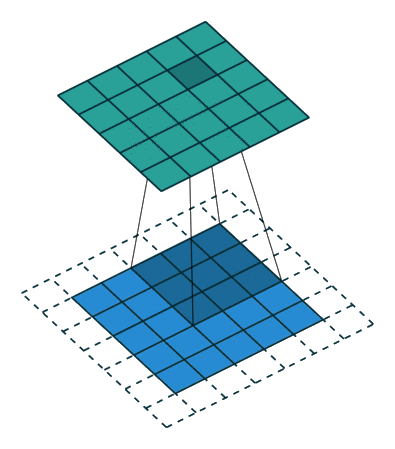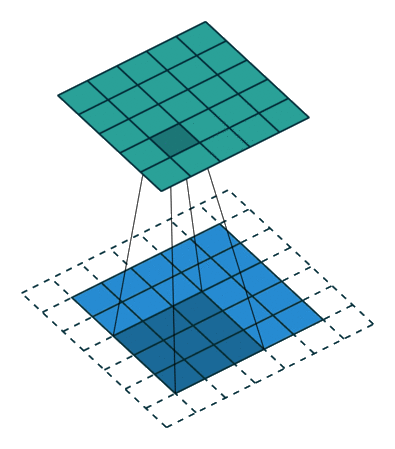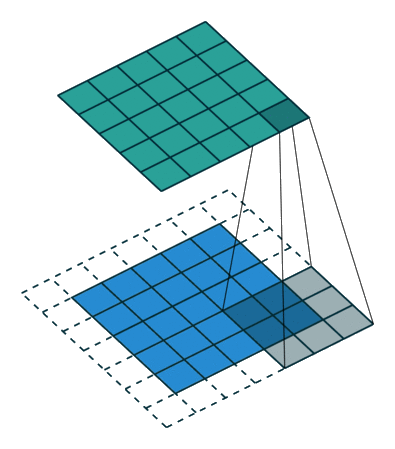

Padding and symmetries
How do the channels look?




Pooling: maxpooling
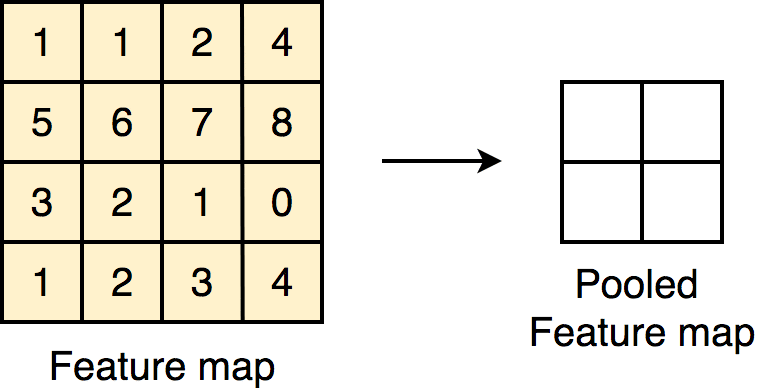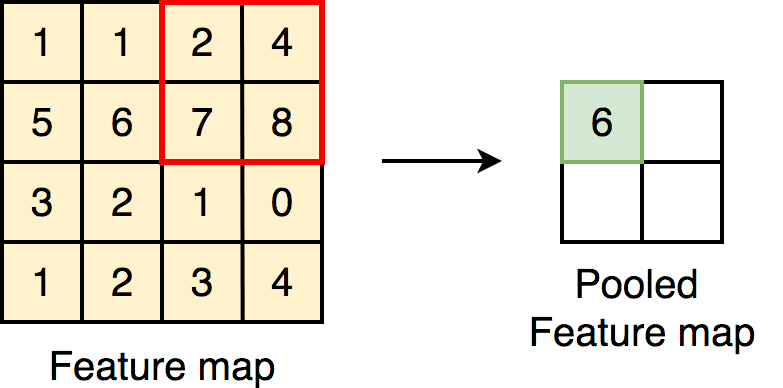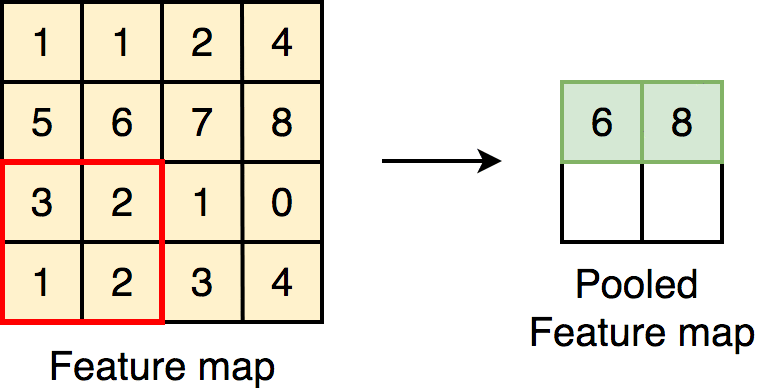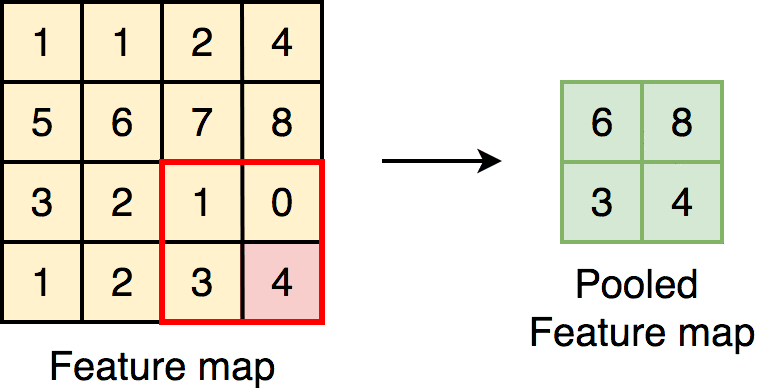
Pooling: maxpooling
Pooling: average
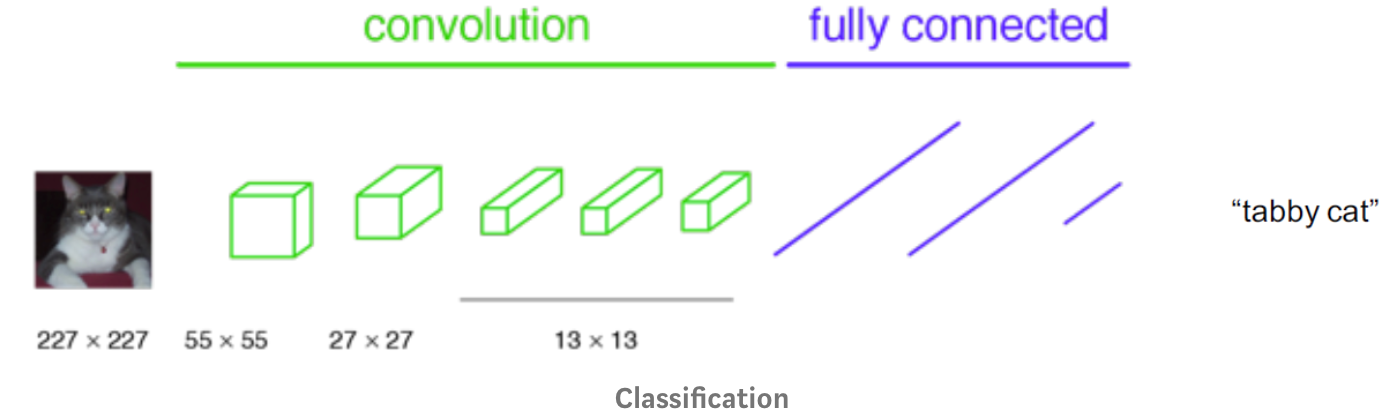
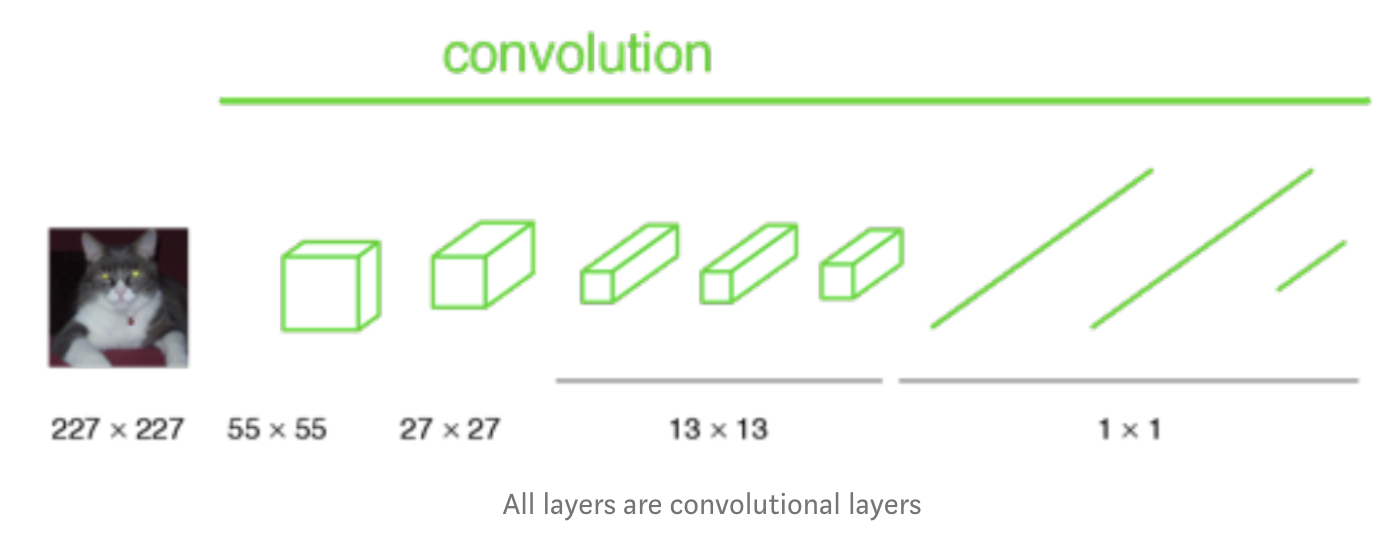
How do we produce a class prediction?
One-convolution

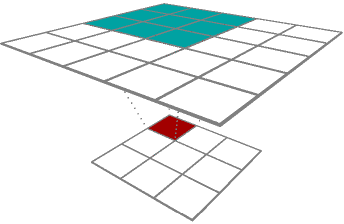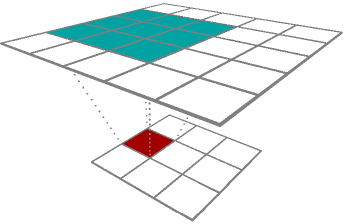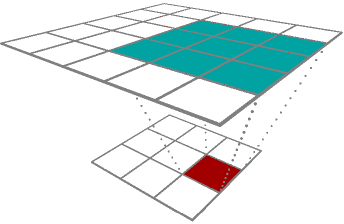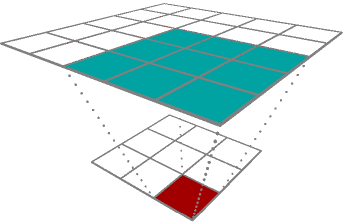
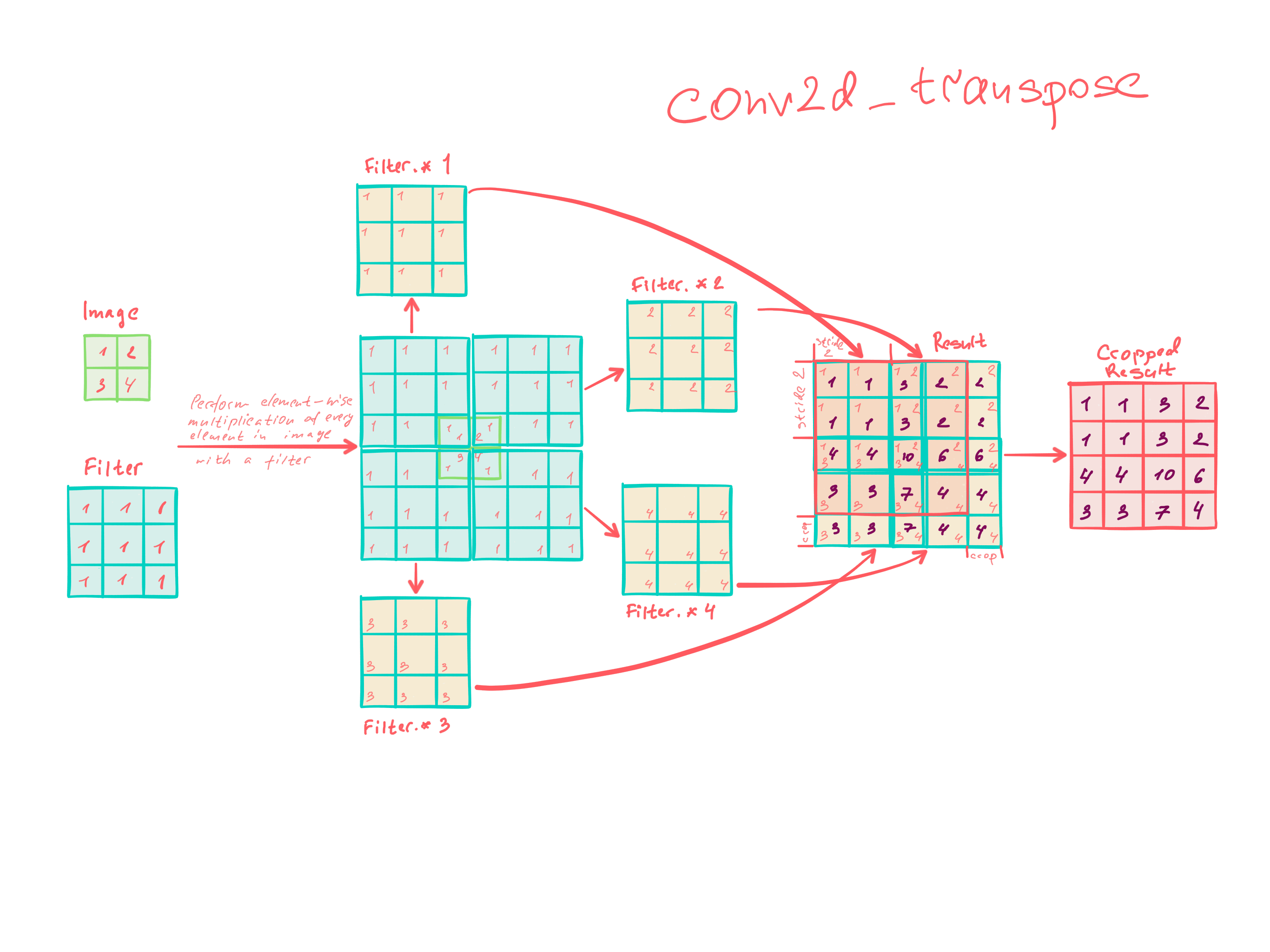
Upconvolution
Dilated convolution
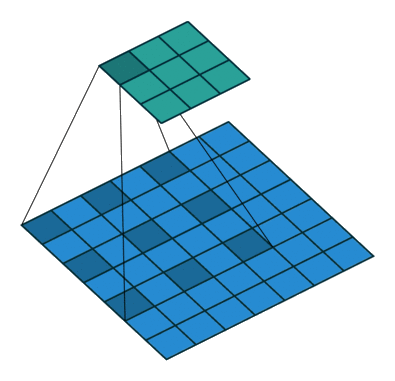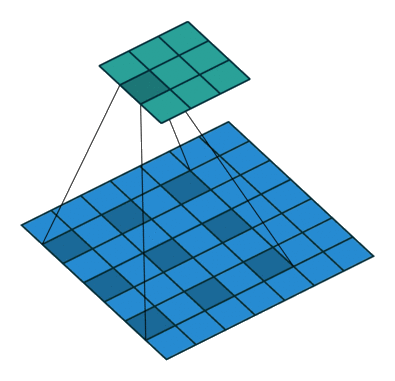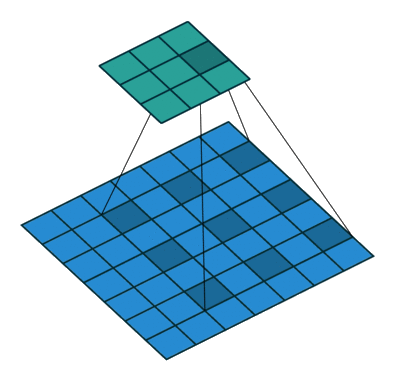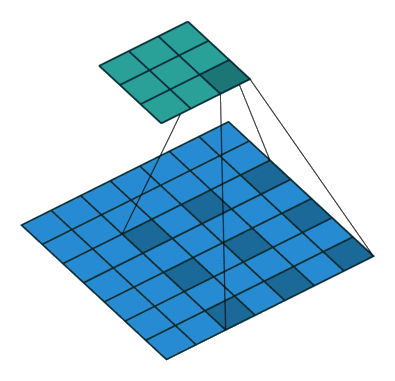
Play with a simulator
Video
Demo
GitHub
Basic building blocks
- Convolution with a filter
- Zero Padding
- Channels and channel-kernel relationship
- Pooling (max and average)
- Moving from convolution layers to predictions
- One convolution
- Upconvolution
- Dilated convolution
Skip connections
Dark knowledge

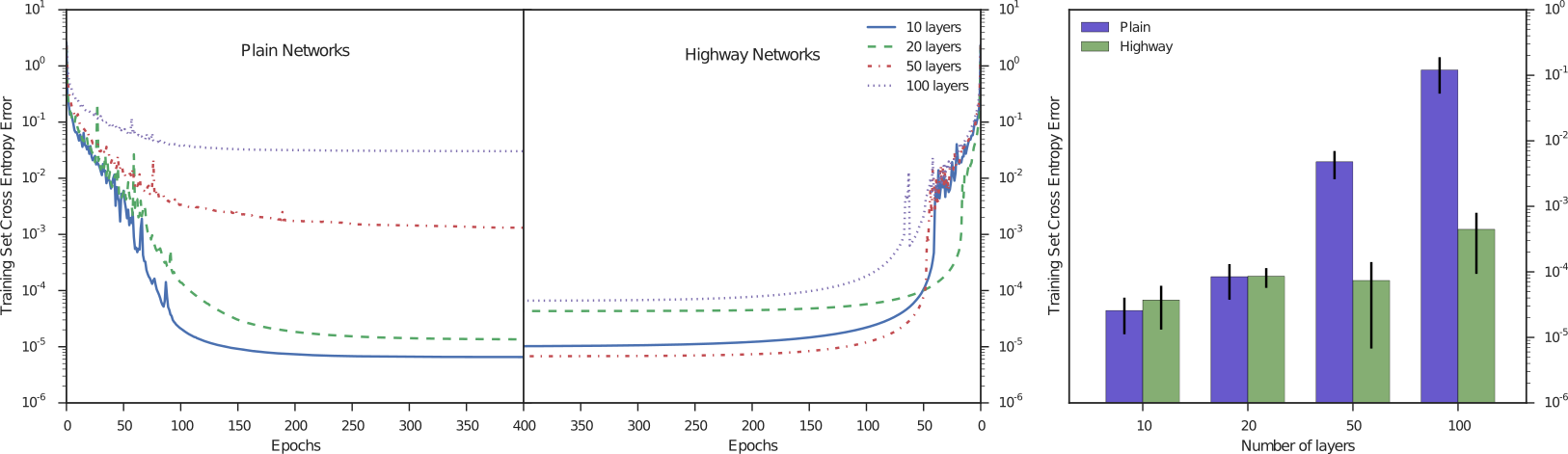
Highway networks (May 2015 on arxiv)
-
$$
\vec{y} = H(\vec{x}, \bm{W}_H)
$$
-
$$
\vec{y} = H(\vec{x}, \bm{W}_H) \odot T(\vec{x}, \bm{W}_T) + \vec{x} \odot C(\vec{x}, \bm{W}_C)
$$
-
$$
\vec{y} = H(\vec{x}, \bm{W}_H) \odot T(\vec{x}, \bm{W}_T) + \vec{x} \odot (1 - T(\vec{x}, \bm{W}_T))
$$
-
$$
\vec{y} =
\left\{
\begin{array}{ll}
\vec{x} & \mbox{if }\;\;T(\vec{x}, \bm{W}_T)=0,\\
H(\vec{x}, \bm{W}_H) & \mbox{if }\;\;T(\vec{x}, \bm{W}_T)=1
\end{array}
\right.
$$
- What if untrained gate is always open and does not let gradients flow?
- Initialize gate biases to large negative values!
Residual Networks (block)
Residual Networks (full)
Residual Networks (performance)
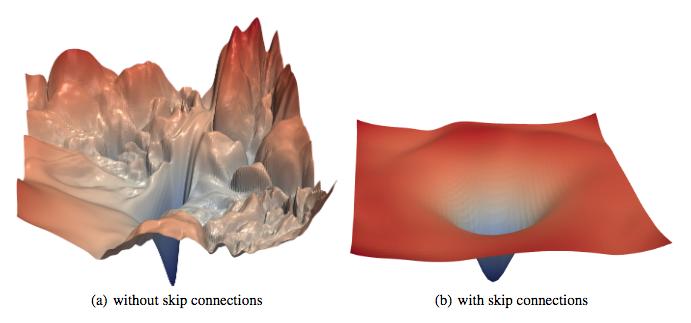
Error surface effect of skip connection
Dense Networks (architecture)
Dense Networks (effect)

Take Away Concepts
- Skip connections
- Gates
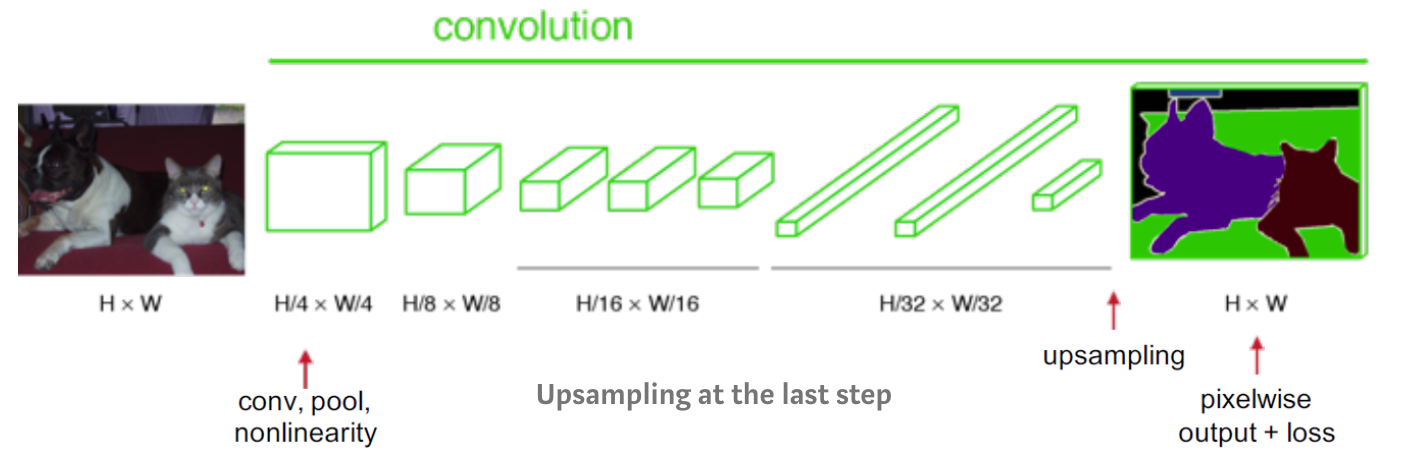
Fully convolutional networks
The task of Semantic segmentation
Semantic segmentation task

Replacing feed forward with convolutional
Fully Convolutional Model (2014)
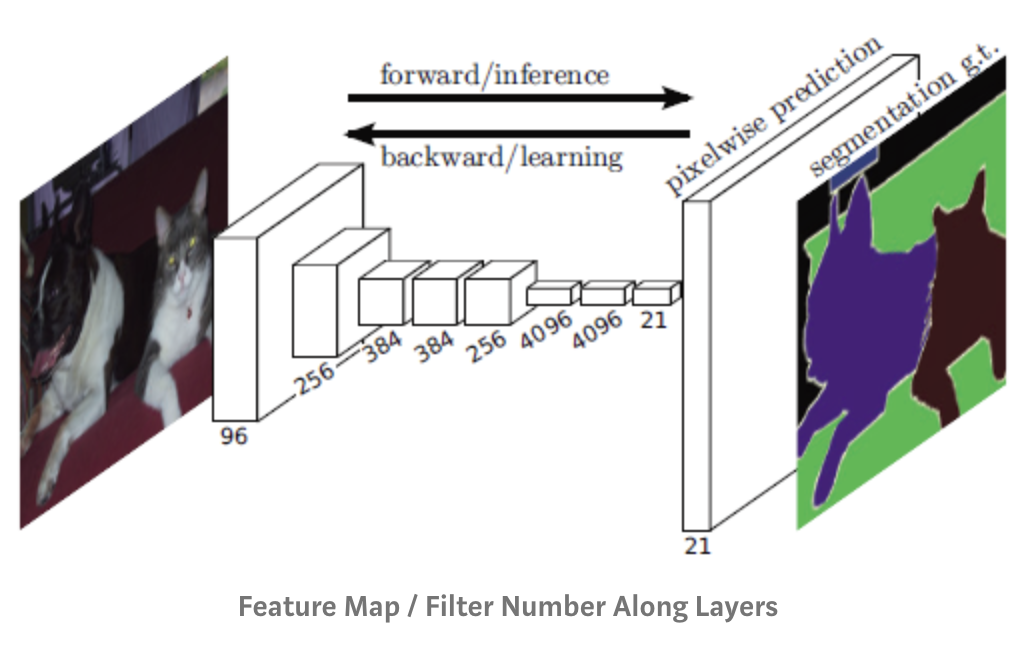
Examples

Take Away Point
- When target and input have the same dimension it may be better to use convolution everywhere.
Semantic segmentation with twists
deep learning standard: U-net
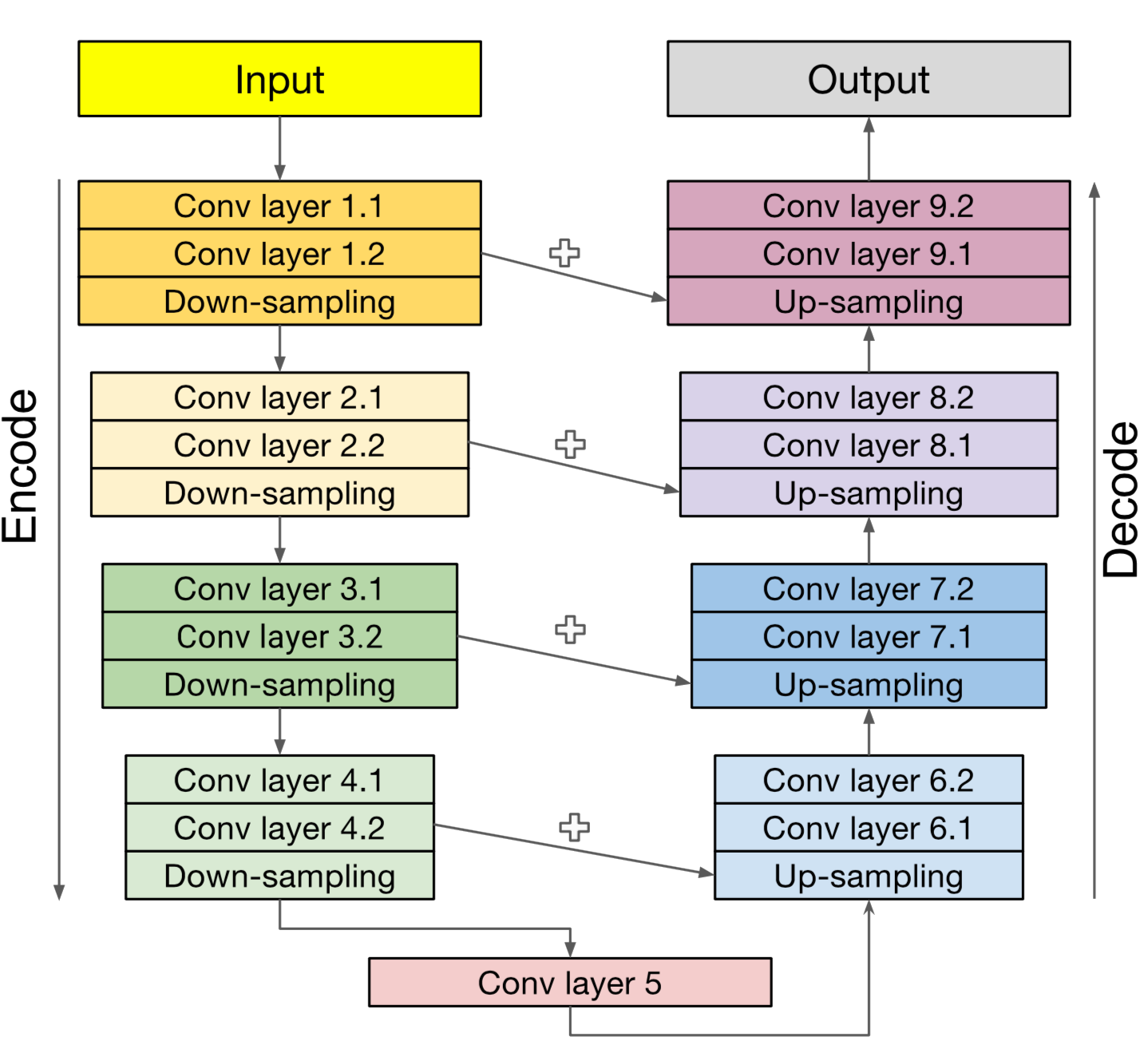
Ronneberger et al. U-net: Convolutional networks
for biomedical image segmentation. MICCAI 2015
Çiçek et al. 3D U-Net: learning dense volumetric segmentation from sparse annotation. MICCAI 2016
Çiçek et al. 3D U-Net: learning dense volumetric segmentation from sparse annotation. MICCAI 2016
deep learning standard: U-net
Ronneberger et al. U-net: Convolutional networks for
biomedical image segmentation. MICCAI 2015
Çiçek et al. 3D U-Net: learning dense volumetric segmentation from sparse annotation. MICCAI 2016
Çiçek et al. 3D U-Net: learning dense volumetric segmentation from sparse annotation. MICCAI 2016
comparison on the brain segmentation task
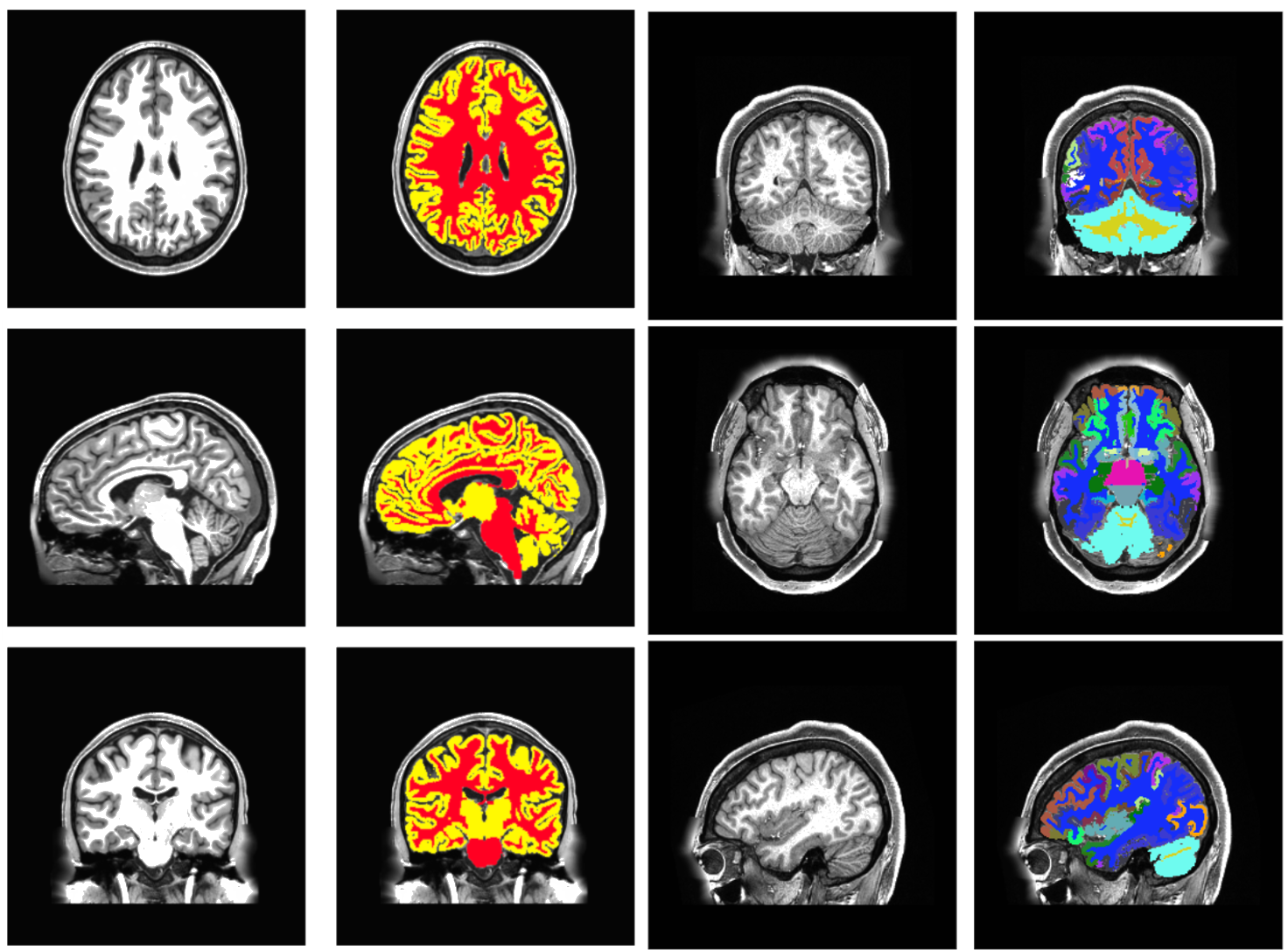
state of the art: freesurfer
Dale et al. Cortical surface-based analysis. I. Segmentation and
surface reconstruction. Neuroimage 1999
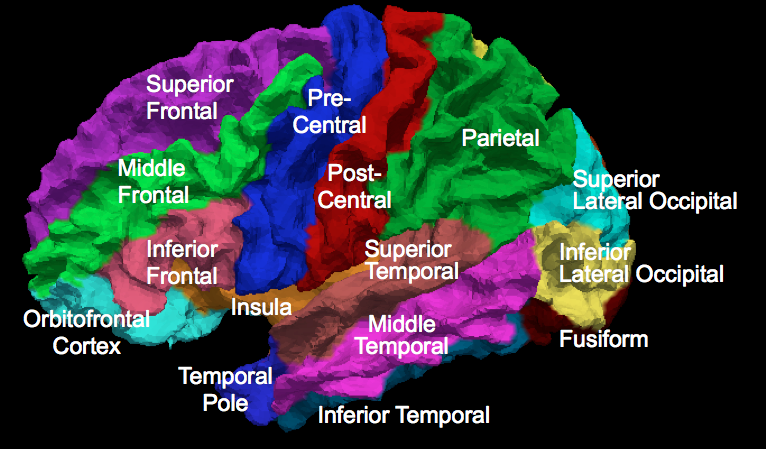
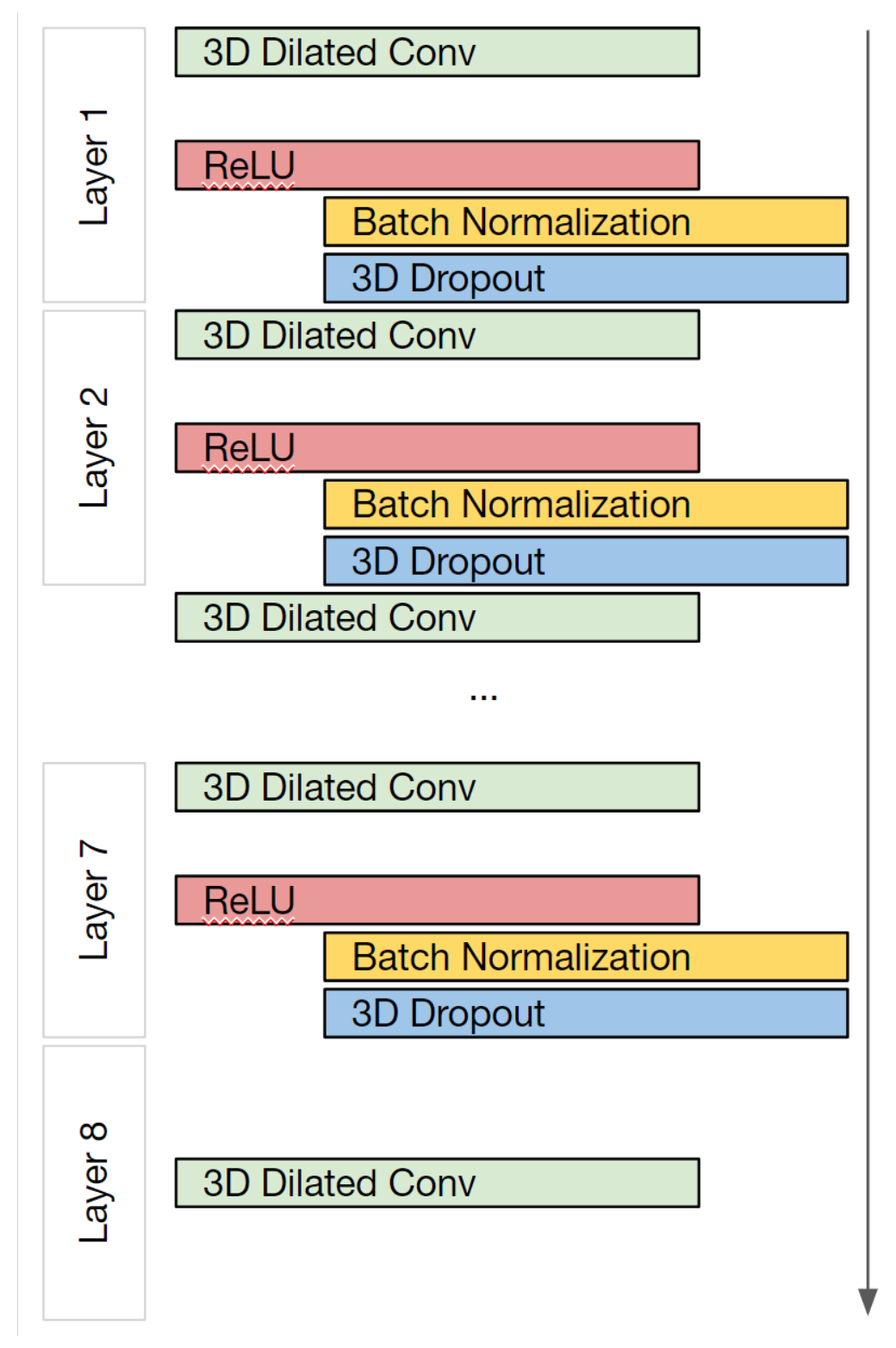
Meshnet
- Gray and White matter
- FreeSurfer for ground truth
- T1 MRIs from HCP
- GitHub
https://github.com/Entodi/MeshNet
Fedorov et al. End-to-end learning of brain tissue segmentation
from imperfect labeling. IJCNN 2017
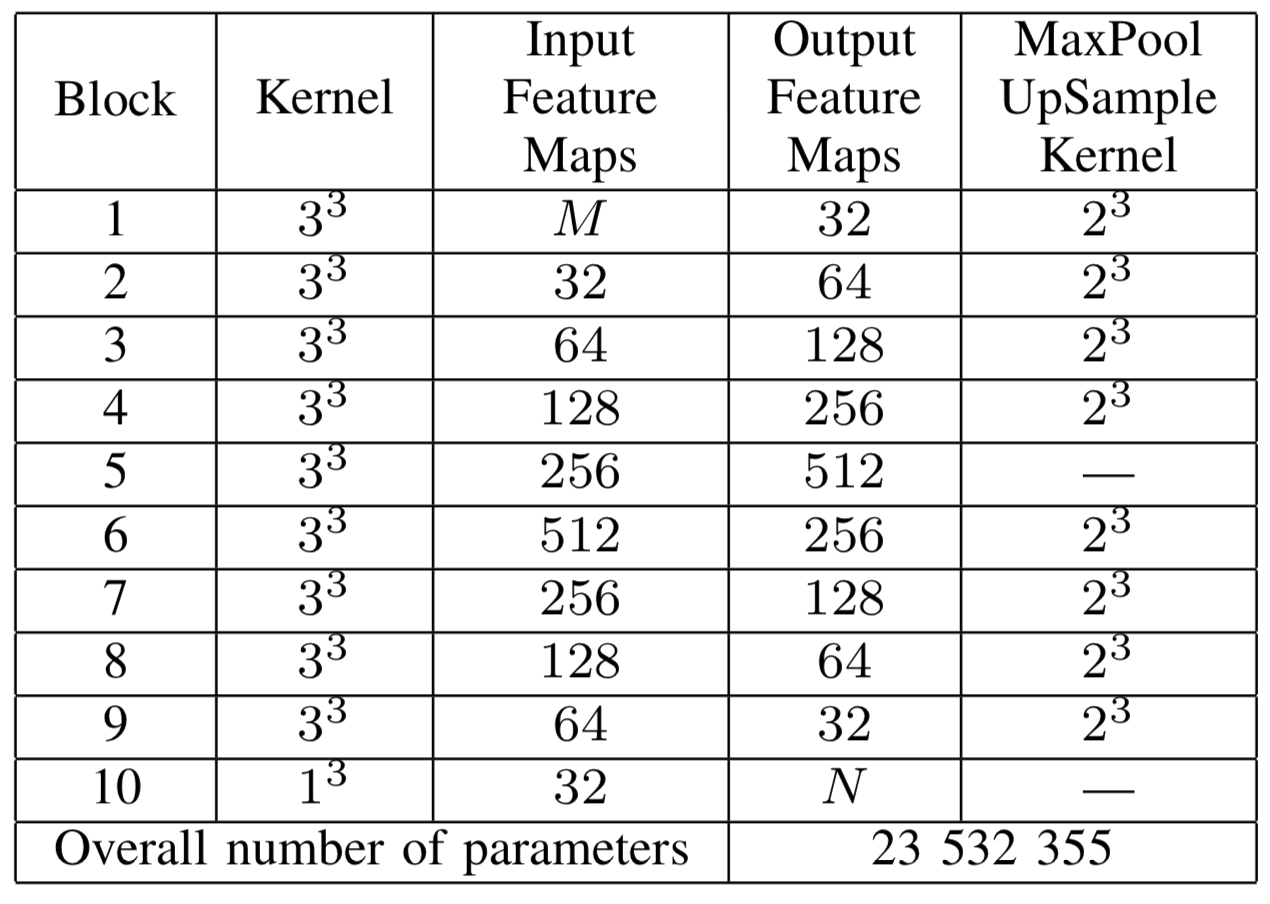
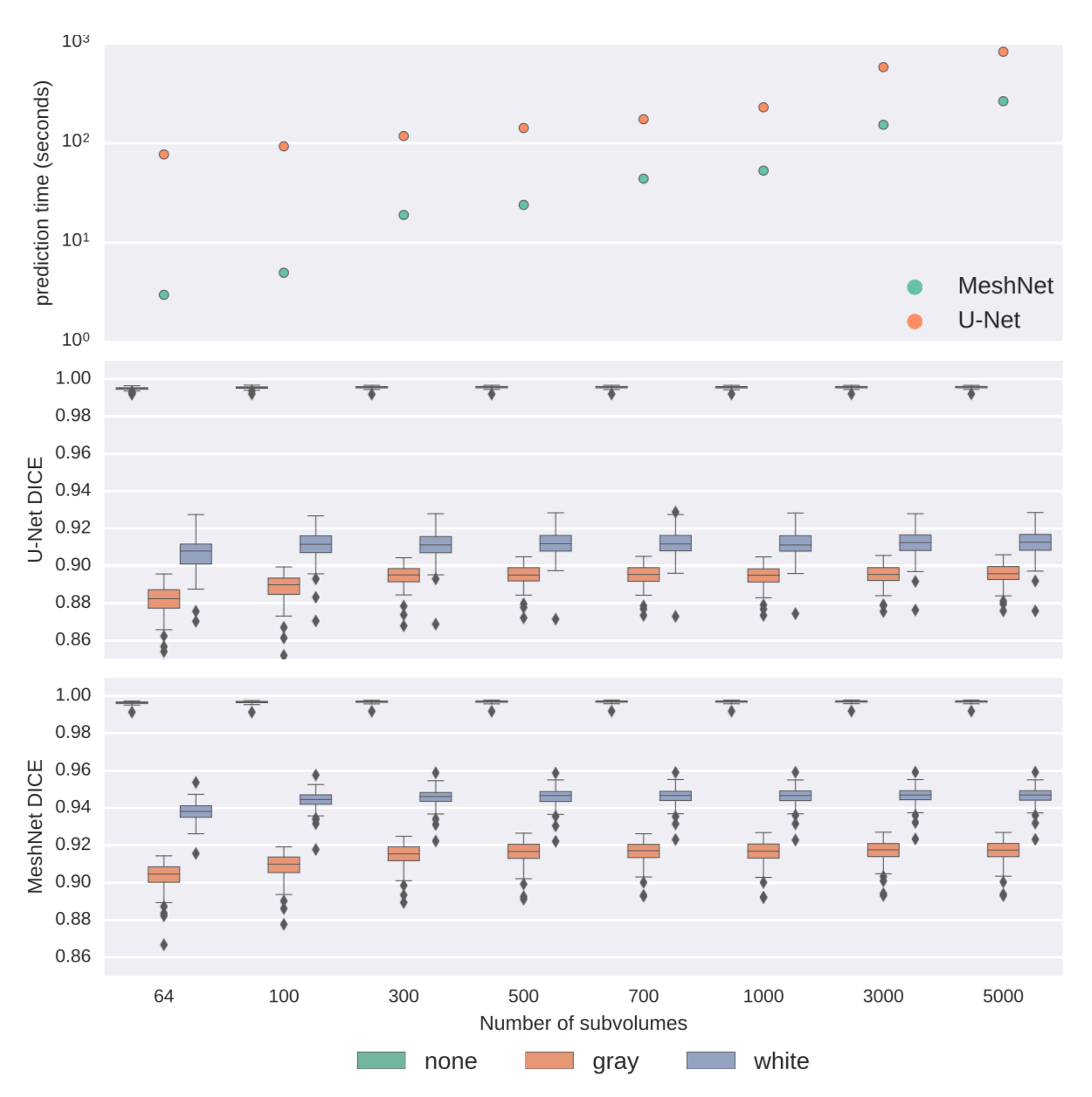
Meshnet
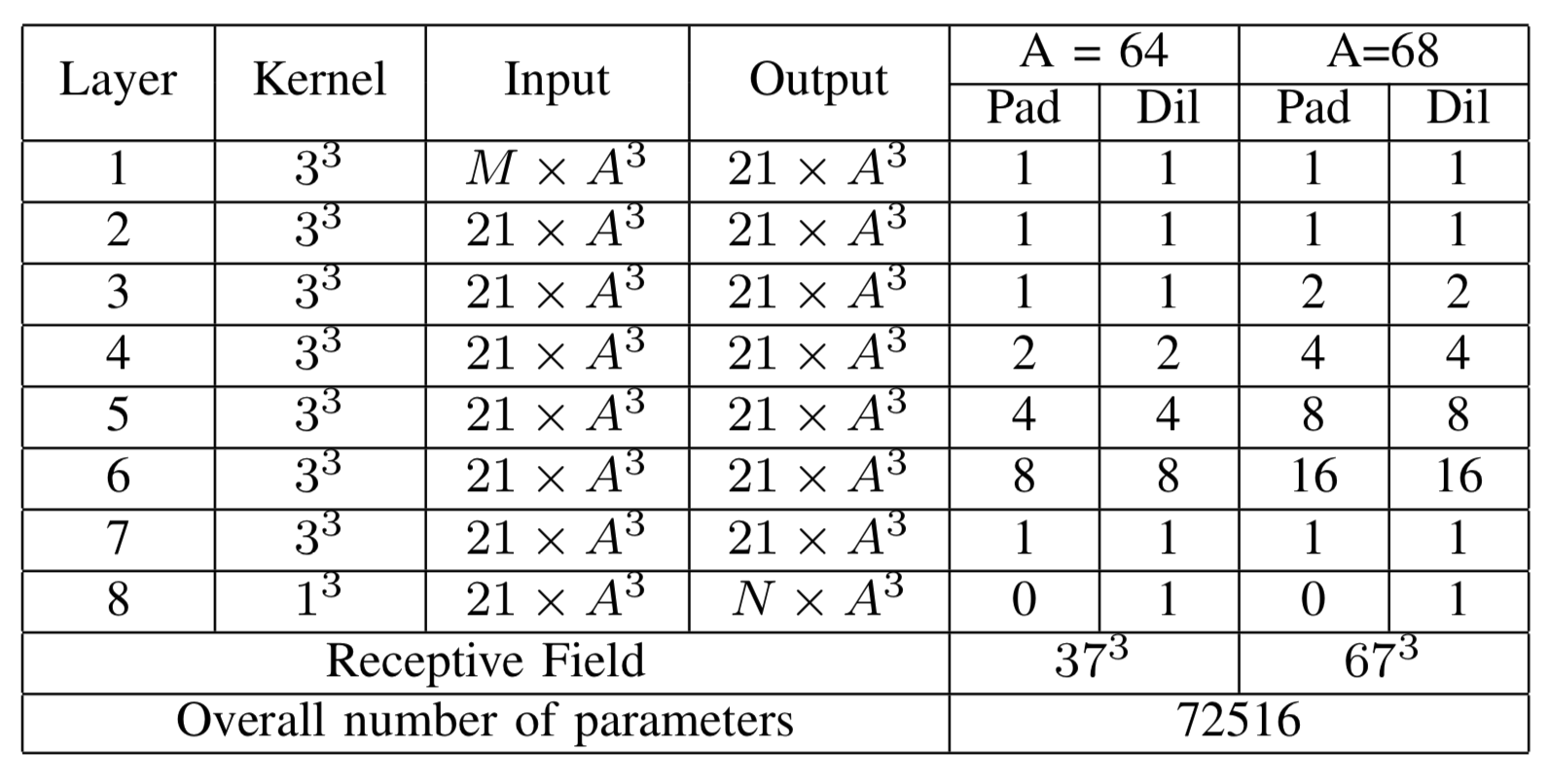
- 72516 vs. 23523355
- 600kb vs. 2Gb
Fedorov et al. End-to-end learning of brain tissue segmentation
from imperfect labeling. IJCNN 2017
Meshnet
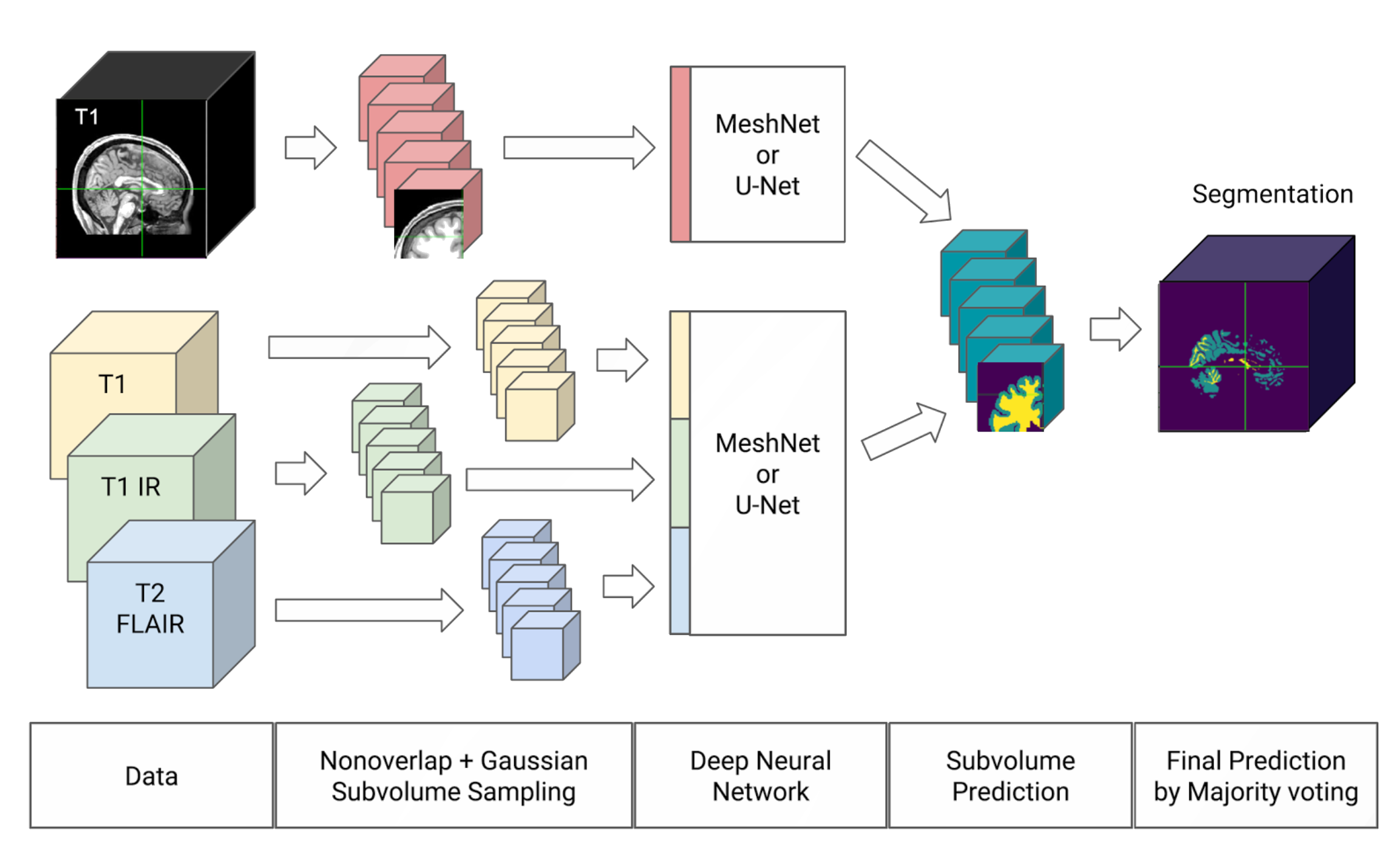
Fedorov et al. End-to-end learning of brain tissue segmentation
from imperfect labeling. IJCNN 2017
Meshnet
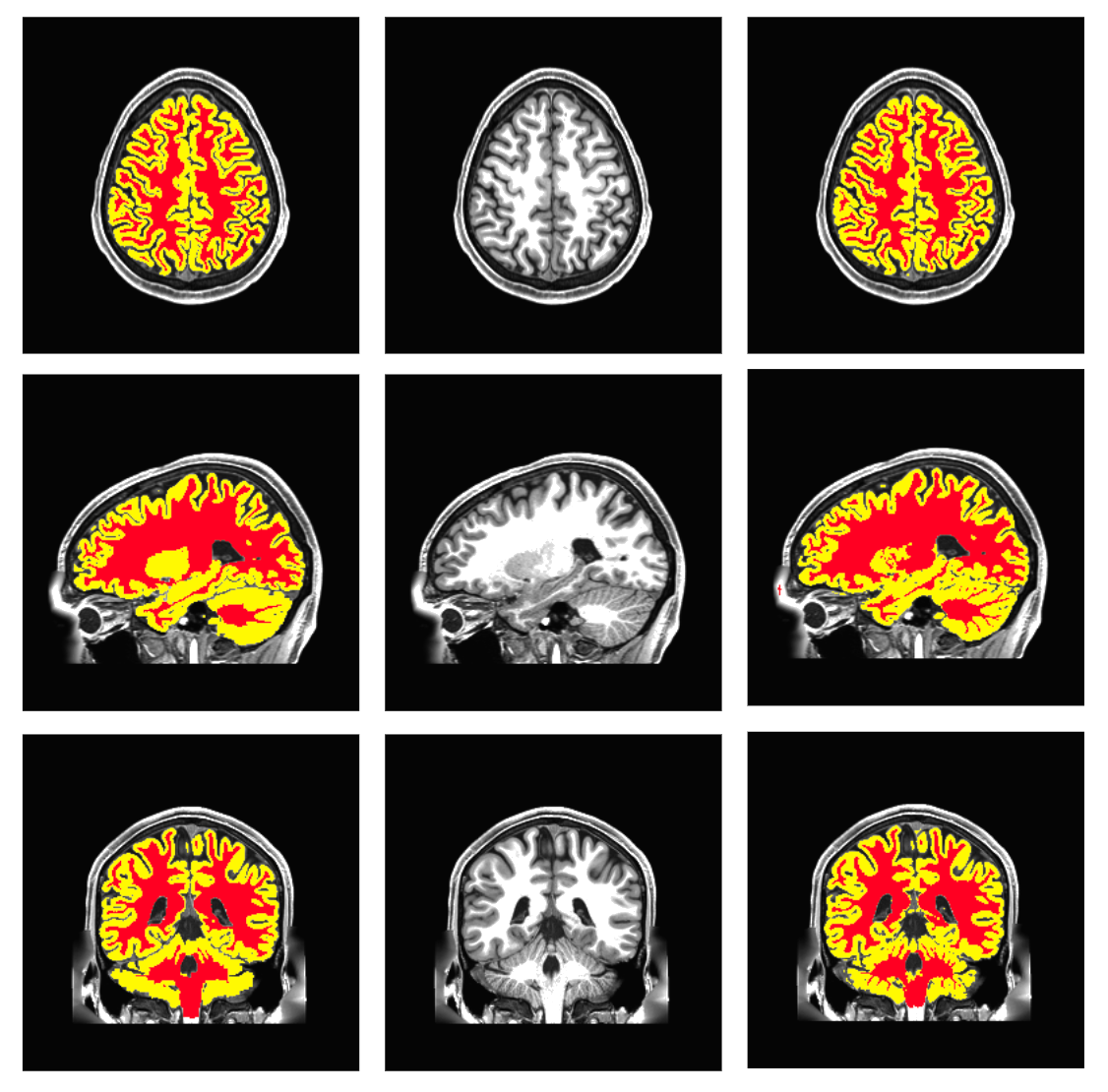
Fedorov et al. End-to-end learning of brain tissue segmentation
from imperfect labeling. IJCNN 2017
(often) better than the teacher
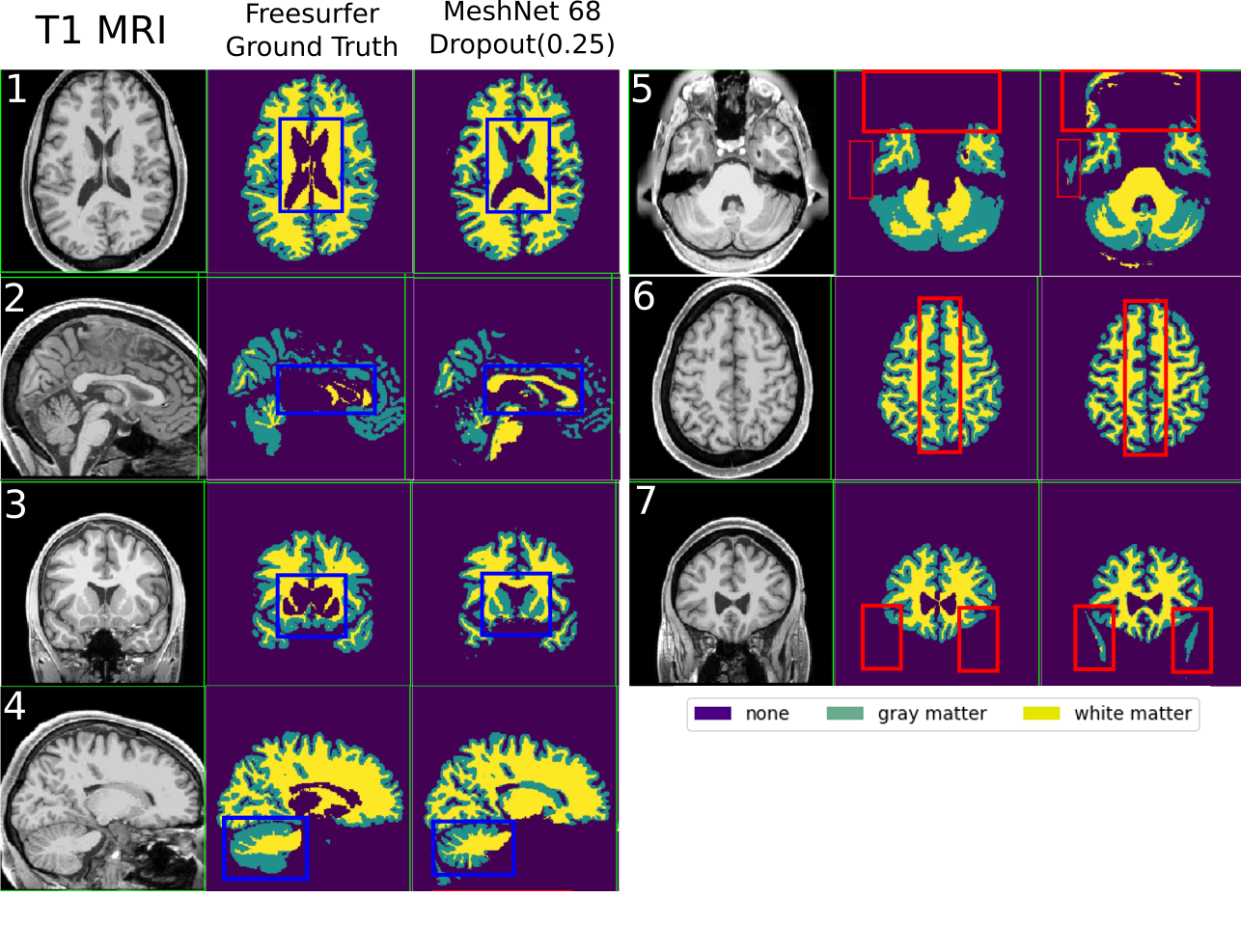
multimodal is straightforward
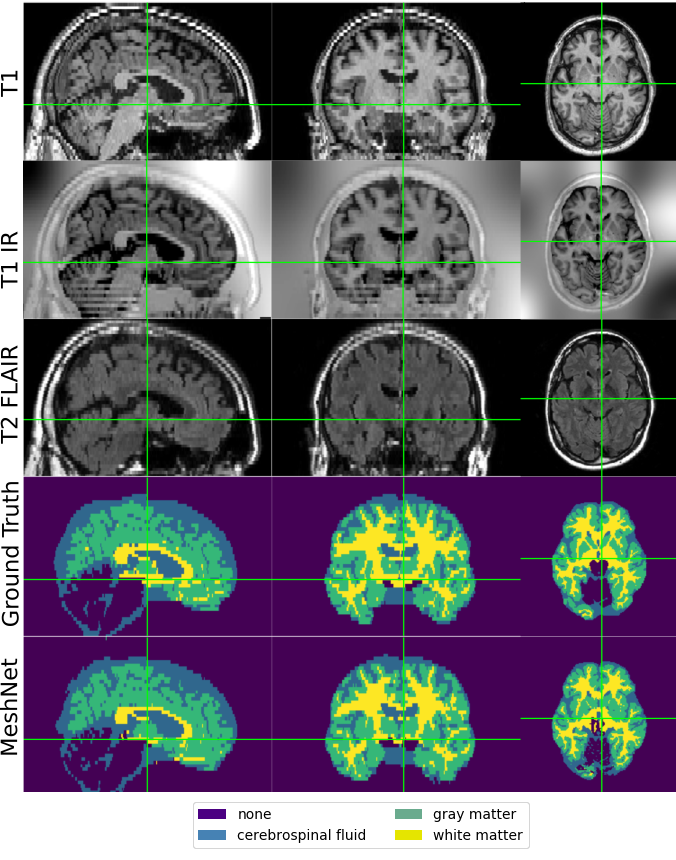
better than the human (sometimes)
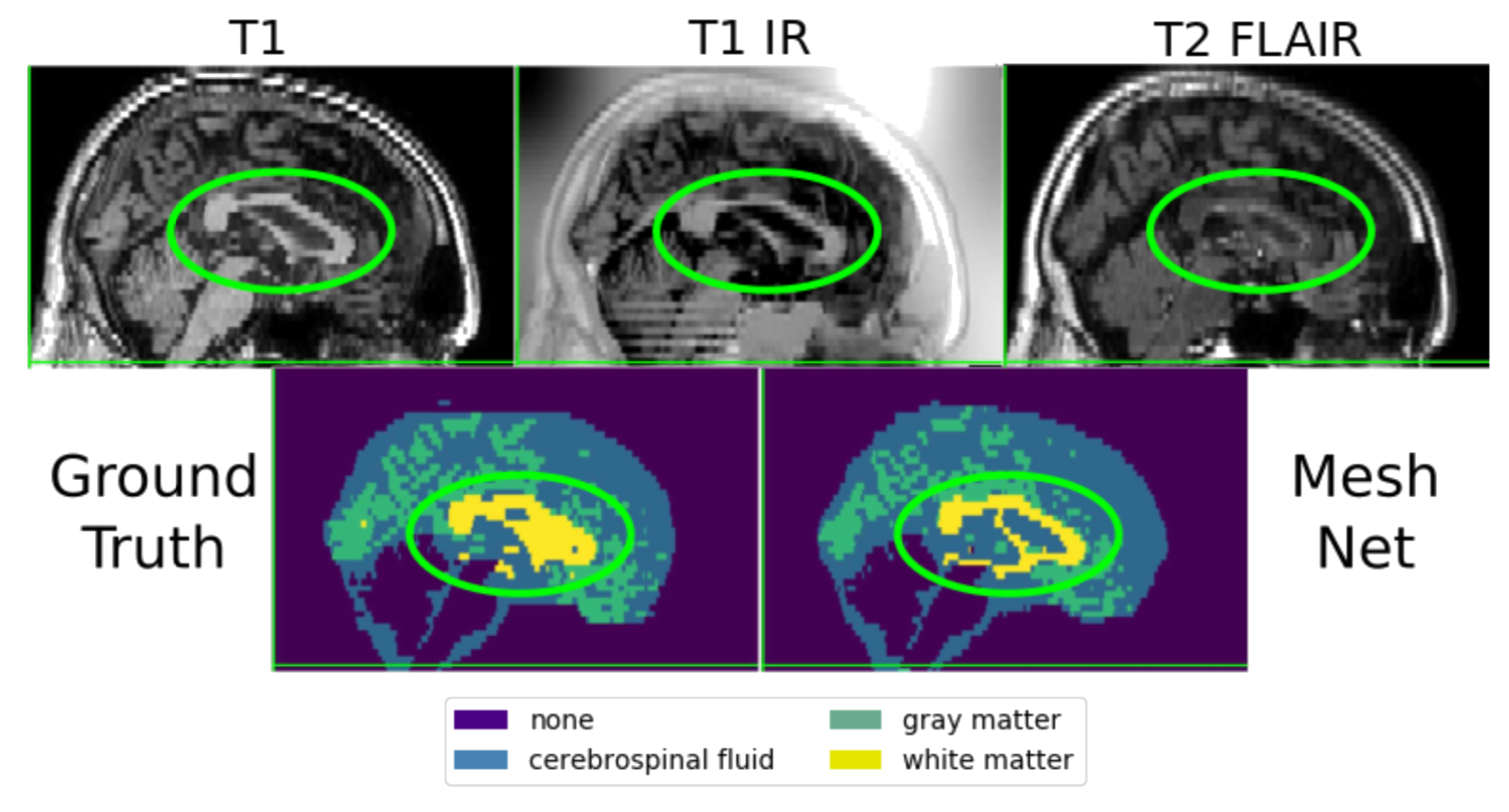
better than U-net
(even more) "Advanced" uses of CNN
Masked Convolutions
PixelCNNs
Wavenet: $\ge$16kHz audio
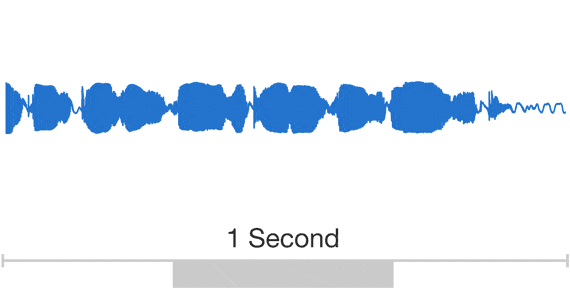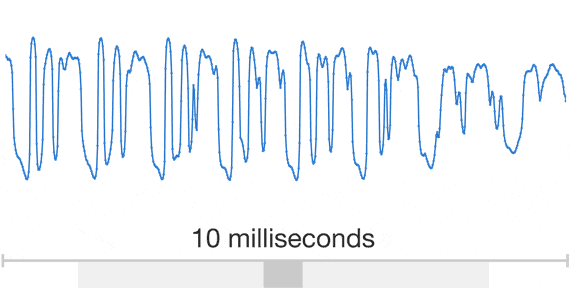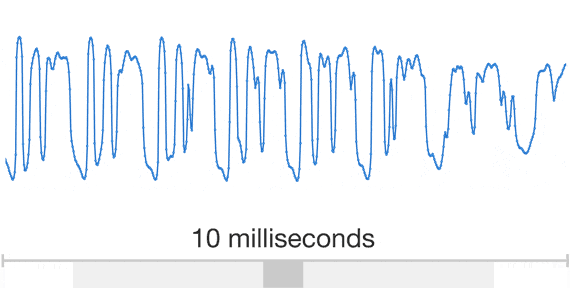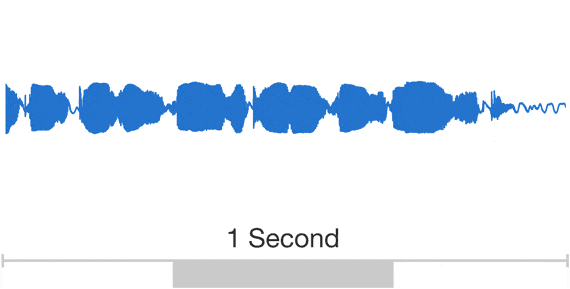
Wavenet: sample by sample

Wavenet: conditioned on text
| Model | "The blue lagoon..." |
|---|---|
| Parametric | |
| Concatenative | |
| Wavenet |
| Model | "English poetry and ..." |
|---|---|
| Parametric | |
| Concatenative | |
| Wavenet |
Deformable Convolutions
Deformable Convolutions

Take Away Points
- Masked convolution
- Pixel based generation
- Deformable convolution (can be rotation invariant)