Advanced Machine Learning

20: Model Comparison I

Outline for the lecture

  • Bias-Variance Trade-off Revisited
  • No Free Lunch Theorem
  • Problems with Accuracy
  • Confusion Matrix

Bias-variance trade off revisited

bandwidth selection for kde

  • Pick $h$ that minimizes the error between the estimated density and the true density
  • Let us use MSE for measuring this error
  • $E\left[ (\prob{P$_{KDE}$}{\vec{x}} - \prob{P}{\vec{x}})^2 \right] $
  • $ = E\left[ \prob{P$_{KDE}$}{\vec{x}}^2 - 2 \prob{P$_{KDE}$}{\vec{x}} \prob{P}{\vec{x}} + \prob{P}{\vec{x}}^2\right]$
  • $ = E\left[ \prob{P$_{KDE}$}{\vec{x}}^2\right] - 2 E\left[\prob{P$_{KDE}$}{\vec{x}}\right] \prob{P}{\vec{x}} + \prob{P}{\vec{x}}^2$
  • Add and subtract $E^2\left[ \prob{P$_{KDE}$}{\vec{x}} \right]$
  • \begin{align} = & E^2\left[ \prob{P$_{KDE}$}{\vec{x}} \right] - 2 E\left[\prob{P$_{KDE}$}{\vec{x}}\right] \prob{P}{\vec{x}} + \prob{P}{\vec{x}}^2 \\ & + E\left[ \prob{P$_{KDE}$}{\vec{x}}^2\right] - E^2\left[ \prob{P$_{KDE}$}{\vec{x}} \right] \end{align}
  • \begin{align} = & (E\left[ \prob{P$_{KDE}$}{\vec{x}} \right] - \prob{P}{\vec{x}})^2 + E\left[ \prob{P$_{KDE}$}{\vec{x}}^2\right] - E^2\left[ \prob{P$_{KDE}$}{\vec{x}} \right] \end{align}
  • This is an example of bias-variance tradeoff

Bias-variance tradeoff

bias variance

Bias-Variance Decomposition for MSE

  • MSE as an error measure
  • $E\left[ (\hat{\theta} - \theta)^2 \right] $
  • $ = E\left[ \hat{\theta}^2 - 2 \hat{\theta}\theta + \theta^2\right]$
  • $ = E\left[ \hat{\theta}^2\right] - 2 E\left[\hat{\theta}\right] \theta + \theta^2$
  • Add and subtract $E\left[ \hat{\theta} \right]^2$
  • \begin{align} = & E\left[ \hat{\theta} \right]^2 - 2 E\left[\hat{\theta}\right] \theta + \theta^2 \\ & + E\left[ \hat{\theta}^2\right] - E\left[ \hat{\theta} \right]^2 \end{align}
  • \begin{align} = & (E\left[ \hat{\theta} \right] - \theta)^2 + E\left[ \hat{\theta}^2\right] - E\left[ \hat{\theta} \right]^2 \end{align}
  • Is not variance $E\left[ (\hat{\theta} - E\left[\hat{\theta}\right])^2\right]$?
  • $E\left[ (\hat{\theta} - E\left[\hat{\theta}\right])^2\right]$
  • $= E\left[ \hat{\theta}^2 - 2\hat{\theta}E\left[\hat{\theta}\right] + E\left[\hat{\theta}\right]^2 \right]$
  • $= E\left[ \hat{\theta}^2 \right] - 2 E\left[ \hat{\theta}\right]E\left[\hat{\theta}\right] + E\left[\hat{\theta}\right]^2$
  • $= E\left[ \hat{\theta}^2 \right] - 2 E\left[\hat{\theta}\right]^2 + E\left[\hat{\theta}\right]^2$
  • $= E\left[ \hat{\theta}^2 \right] - E\left[\hat{\theta}\right]^2$

if data is all we have

how do we know if we're doing well?

how do we know which model is better?

split

Bias-variance tradeoff

bias variance
polyfit

Bias-variance tradeoff

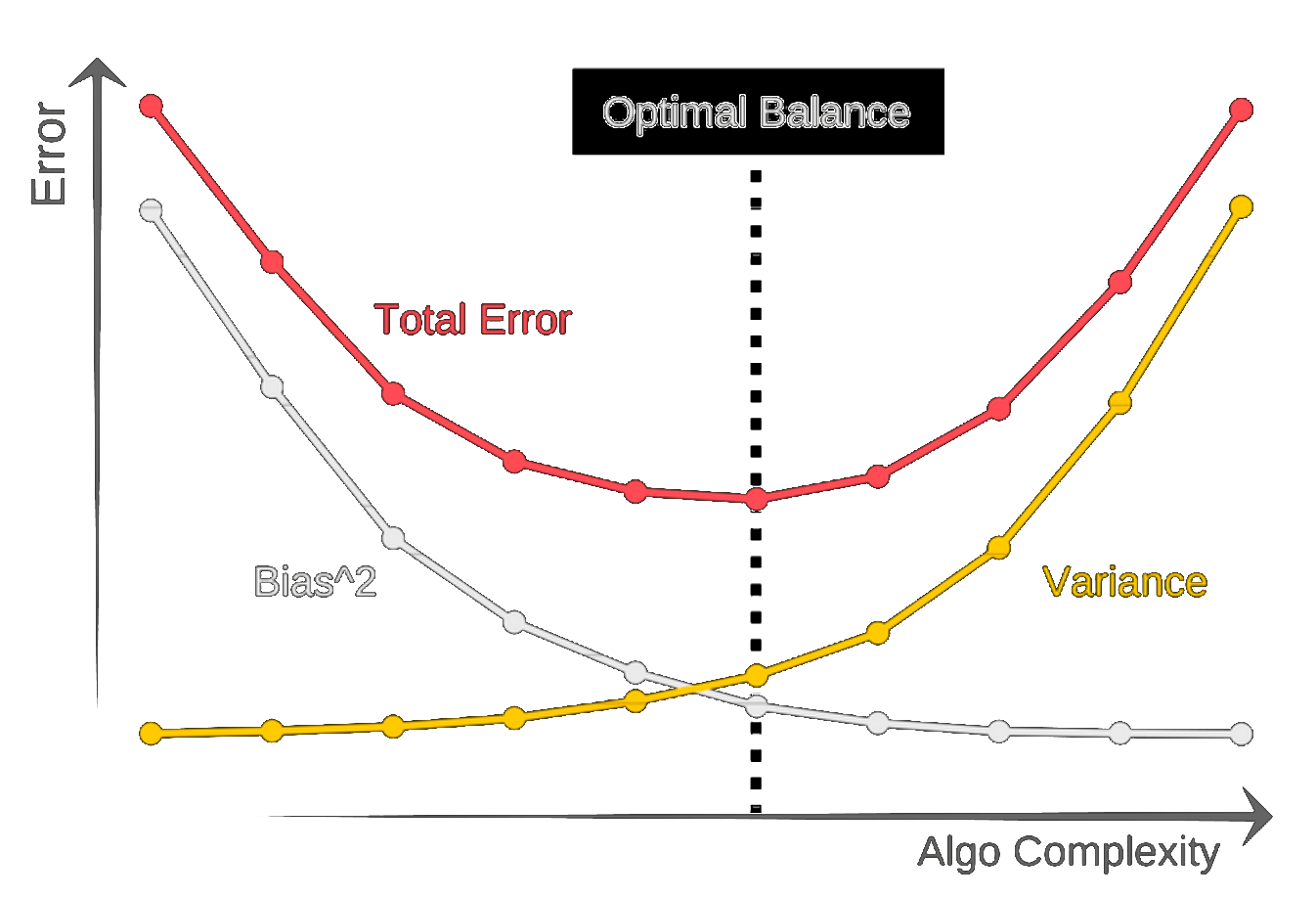
model complexity

Select a model that generalizes best

$E\left[ (g(\theta; {\cal D}) - G(\theta))^2 \right] = \mbox{bias of }g + \mbox{ variance of }g$,
where $g$ is estimated and $G$ is true generalization error
unbiased low variance
On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation

Bias-variance tradeoff

Double-descent curve

double descent
Reconciling modern machine learning practice and the bias-variance trade-of

No free lunch theorem

remote
cats and mice
Кошки-мышки (rat's n cats)
"Even after the observation of the frequent conjunction of objects, we have no reason to draw any inference concerning any object beyond those of which we have had experience."

David Hume, in A Treatise of Human Nature, Book I, part 3, Section 12.

David Wolpert
wolperts
The Lack of A Priori Distinction Between Learning Algorithms and No Free Lunch Theorems for Optimization

No free lunch theorem (simply put)

There is not a universally good algorithms that's best on all possible test data!

Problems with accuracy

Confusion Matrix

insilico