Advanced Machine Learning

19: Manifold Learning

Outline for the lecture

  • Motivation
  • Multidimensional Scaling
  • LLE
  • IsoMap
  • t-SNE
  • Random Projections

Motivation

Data is inherently low dimensional

millions of dimensions

millions of inputs

Exploratory data analysis

  • Find hidden low dimensional structure in the data
  • Low dimensional representation for visualization

plot your data

Manifolds

Informally: any object nearly flat on small scales
1D 2D

Manifold learning

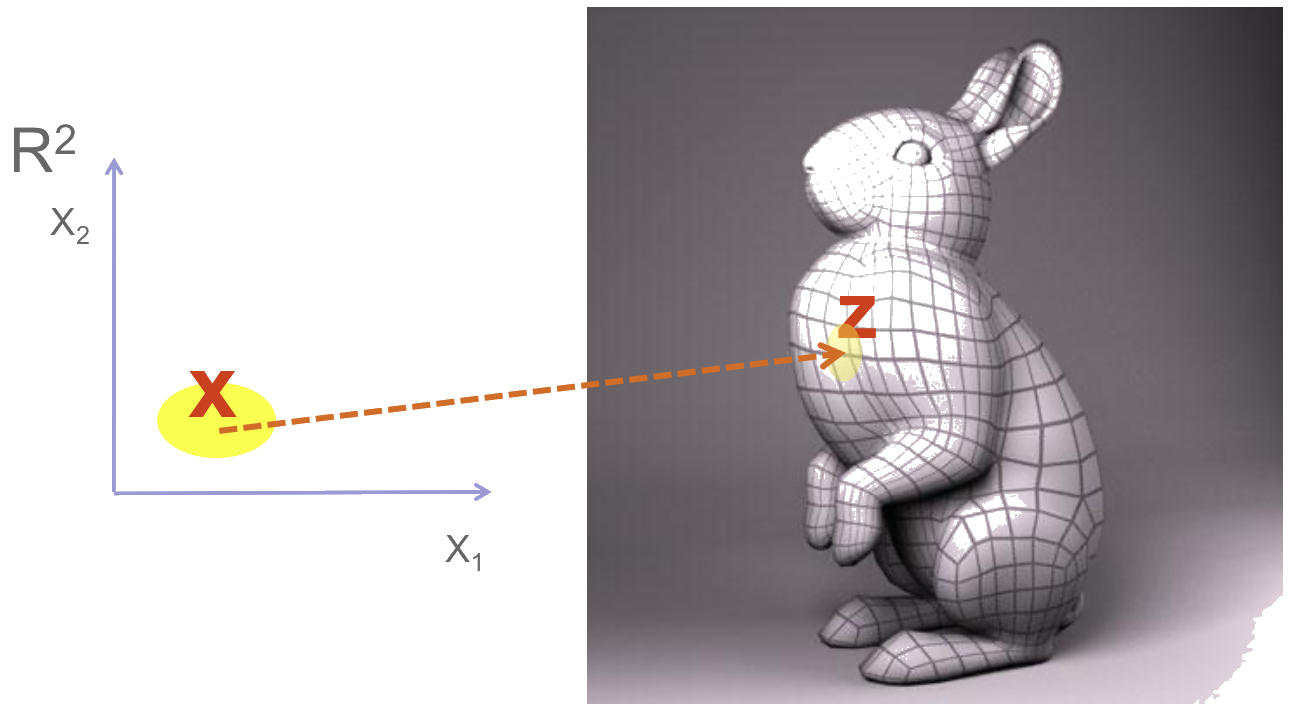
rabbit

local mapping

https://pair-code.github.io/understanding-umap/

Manifold learning Algorithms

  • PCA (1901)
  • Multi-dimensional Scaling (1952)
  • Sammon mapping (1969)
  • Maximum Variance Unfolding
  • Locally Linear Embedding (2000)
  • Isomap (2000)
  • Laplacian Eigenmaps (2003)
  • t-distributed Stochastic Neighbor Embedding (tSNE)
  • Random Projections
  • many more

Let's see how they work

pull

Under construction starting here

lego

Multidimensional Scaling

IsoMap

Locally Linear Embedding

t-SNE

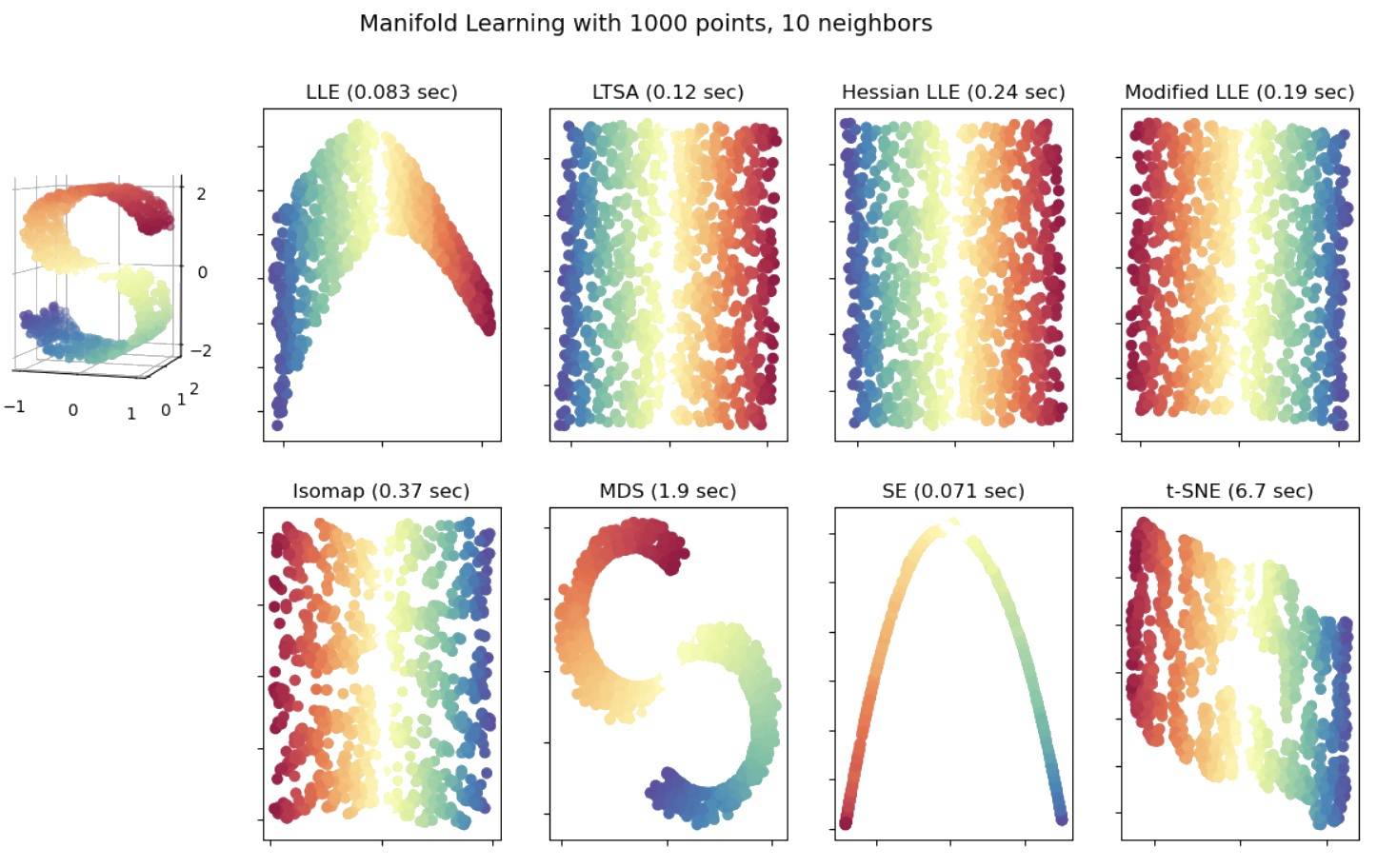
Algorithms compared on Swiss Roll

all
sk-learn documentation
also, see this

Random Projections

Johnson-Lindenstrauss Theorem

Key Idea: Random projections can approximately preserve distances between points in high-dimensional space when mapped to a lower-dimensional space.

Theorem Statement

For any 0 < ε < 1 and any set of n points in ℝd, there exists a linear map f: ℝd → ℝk, where:

k = O(log(n) / ε2)

such that for all points u and v:

(1 - ε) ||u - v||2 ≤ ||f(u) - f(v)||2 ≤ (1 + ε) ||u - v||2

Implications

  • Enables dimensionality reduction while preserving approximate distances.
  • Useful for high-dimensional data analysis and machine learning.
  • Key technique for manifold learning and embedding methods.