Advanced Machine Learning
15: Stochastic Gradient Descent
Schedule
| # | date | topic | description |
|---|---|---|---|
| 1 | 22-Aug-2022 | Introduction | |
| 2 | 24-Aug-2022 | Foundations of learning | |
| 3 | 29-Aug-2022 | PAC learnability | |
| 4 | 31-Aug-2022 | Linear algebra (recap) | hw1 released |
| 05-Sep-2022 | Holiday | ||
| 5 | 07-Sep-2022 | Linear learning models | |
| 6 | 12-Sep-2022 | Principal Component Analysis | project ideas |
| 7 | 14-Sep-2022 | Curse of Dimensionality | hw1 due |
| 8 | 19-Sep-2022 | Bayesian Decision Theory | hw2 release |
| 9 | 21-Sep-2022 | Parameter estimation: MLE | |
| 10 | 26-Sep-2022 | Parameter estimation: MAP & NB | finalize teams |
| 11 | 28-Sep-2022 | Logistic Regression | |
| 12 | 03-Oct-2022 | Kernel Density Estimation | |
| 13 | 05-Oct-2022 | Support Vector Machines | hw3, hw2 due |
| 10-Oct-2022 | * Mid-point projects checkpoint | * | |
| 12-Oct-2022 | * Midterm: Semester Midpoint | exam | |
| 14 | 17-Oct-2022 | Matrix Factorization | |
| 15 | 19-Oct-2022 | Stochastic Gradient Descent |
| # | date | topic | description |
|---|---|---|---|
| 16 | 24-Oct-2022 | k-means clustering | |
| 17 | 26-Oct-2022 | Expectation Maximization | hw4, hw3 due |
| 18 | 31-Oct-2022 | Automatic Differentiation | |
| 19 | 02-Nov-2022 | Nonlinear embedding approaches | |
| 20 | 07-Nov-2022 | Model comparison I | |
| 21 | 09-Nov-2022 | Model comparison II | hw5, hw4 due |
| 22 | 14-Nov-2022 | Model Calibration | |
| 23 | 16-Nov-2022 | Convolutional Neural Networks | |
| 21-Nov-2022 | Fall break | ||
| 23-Nov-2022 | Fall break | ||
| 24 | 28-Nov-2022 | Word Embedding | hw5 due |
| 30-Nov-2022 | Presentation and exam prep day | ||
| 02-Dec-2022 | * Project Final Presentations | * | |
| 07-Dec-2022 | * Project Final Presentations | * | |
| 12-Dec-2022 | * Final Exam | * | |
| 15-Dec-2022 | Grades due |
Outline for the lecture
- Stochastic Gradient Descent
Stochastic Gradient Descent
heavily based on Sebastian Ruder's slides for An overview of gradient descent optimization algorithms
Gradient Descent
A way to minimize an objective function $\prob{J}{\theta}$
- $\prob{J}{\theta}$: Objective function
- $\theta \in \RR^d$: parameters of the model
- $\eta$: Learning rate that determines the size of steps we take
Update Equation
$\theta = \theta - \eta \nabla_{\theta} \prob{J}{\theta}$
Gradient Descent Variants
There are 3 of them
- Batch gradient descent
- Stochastic gradient descent
- Mini-batch gradient descent
Update Equation
$\theta = \theta - \eta {\color{red} \nabla_{\theta} \prob{J}{\theta}}$
The red term is different for each method
Trade Off
Depending on the amount of data
- The accuracy of the parameter update
- The time is takes to perform an update
| Method | Accuracy | Time | Memory | Online |
|---|---|---|---|---|
| Batch | slow | high | ||
| Stochastic | fast | low | ||
| Mini-batch | moderate | moderate |
Batch gradient descent
Compute the gradient of $\prob{J}{\theta}$ with respect to the entire dataset
Update Equation
$\theta = \theta - \eta \nabla_{\theta} \prob{J}{\theta}$
We need to calculate the gradients for the whole dataset to perform just one update.
for i in range(number_of_epochs):
gradient = eval_gradient(loss_fun, data, parameters)
parameters = parameters - eta * gradient
Batch gradient descent
Advantages
- We're working with the best possible error surface
- Guaranteed to converge to a local or global minimum of that surface
Disadvantages
- Can be very slow
- Can be intractable due to memory requirements
- No online updates
Stochastic gradient descent
Perform a parameter update for each training example $\vec{x}_i$ and the corresponding label $y_i$
Update Equation
$\theta = \theta - \eta \nabla_{\theta} \prob{J}{\theta; \vec{x}_i; y_i}$
We need to evaluate the gradient only for a single data sample.
for i in range(number_of_epochs):
np.random.shuffle(data)
for example in data:
gradient = eval_gradient(loss_fun, example, parameters)
parameters = parameters - eta * gradient
Stochastic gradient descent
Advantages
- It is usually much faster than batch gradient descent.
- It can be used to learn online.
Disadvantages
- It performs frequent updates with a high variance that cause the objective function to fluctuate heavily.
The fluctuations
- Batch gradient descent converges to the minimum of the basin the parameters are placed in and the fluctuation is small.
- SGD’s fluctuation is large but it enables to jump to new and potentially better local minima.
- However, this ultimately complicates convergence to the exact minimum, as SGD will keep overshooting
learning rate annealing
When we slowly decrease the learning rate, SGD shows the same convergence behaviour as batch gradient descent
Mini-batch gradient descent
Perform an update on a small sample of data
Update Equation
$\theta = \theta - \eta \nabla_{\theta} \prob{J}{\theta; \vec{x}_{i:i+n}; y_{i:i+n}}$
for i in range(number_of_epochs):
np.random.shuffle(data)
for batch in batch_iterator(data, batch_size=32):
gradient = eval_gradient(loss_fun, batch, parameters)
parameters = parameters - eta * gradient
Mini-batch gradient descent
Advantages
- Reduces the variance of the parameter updates.
- Can make use of highly optimized matrix optimizations common to deep learning libraries that make computing the gradient very efficiently.
Disadvantages
- We have to set the mini-batch size
Challenges
- How to set the learning rate
- How to set the learning rate schedule
- How to change the learning rate per parameter
- How to avoid local minima and saddle points
Batch?
Gradient descent optimization algorithms
- Momentum
- Nesterov accelerated gradient
- Adagrad
- RMSprop
- Adadelta
- Adam
SGD problems
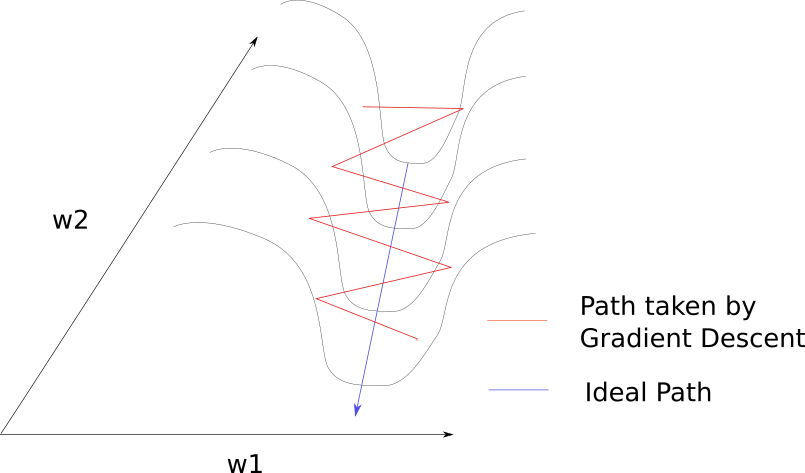
Let's look at a simple demo
Momentum
\begin{align*} \vec{v}_t & = \gamma \vec{v}_{t-1} + \eta \nabla_{\theta} \prob{J}{\theta}\\ \vec{\theta} &= \vec{\theta} - \vec{v}_t \\ \gamma &\simeq 0.9 \end{align*}
Momentum is accumulated the farther the ball rolls downhill
Let's see the demo again
Let's see the demo again
Nesterov accelerated gradient
when we want to do better than that
\begin{align*} \vec{v}_t & = \gamma \vec{v}_{t-1} + \eta \nabla_{\theta} \prob{J}{\theta - \gamma \vec{v}_{t-1}}\\ \vec{\theta} &= \vec{\theta} - \vec{v}_t \\ \gamma &\simeq 0.9 \end{align*}
AdaGrad
we want parameter-specific learning rate
\begin{align*} \vec{v}_t & = \vec{v}_{t-1} + (\nabla_{\theta} \prob{J}{\vec{\theta}})^2\\ \vec{\theta} &= \vec{\theta} - \frac{\eta}{\sqrt{{\prob{diag}{\vec{v}_t} + \epsilon}}} \nabla_{\theta} \prob{J}{\vec{\theta}} \\ \end{align*}
RMSprop: stop diminishing learning rate
\begin{align*} \vec{g}_t & = \nabla_{\theta} \prob{J}{\vec{\theta}} \\ \prob{E}{\vec{g}^2}_t & = \gamma\prob{E}{\vec{g}^2}_{t-1} + (1-\gamma)\vec{g}_t^2\\ \vec{\theta} &= \vec{\theta} - \frac{\eta}{\sqrt{{\prob{diag}{\prob{E}{\vec{g}^2}_t} + \epsilon}}} \vec{g}_t \\ \end{align*}
\begin{align*} \mbox{units of}\, \Delta\vec{\theta} \propto \mbox{units of } \vec{g} \propto \mbox{units of } \frac{\partial J}{\partial \vec{\theta}}\propto \frac{1}{\mbox{units of}\, \vec{\theta}}\\ \mbox{but} \quad \Delta\vec{\theta} \propto \mathbf{H}^{-1}\vec{g} \propto \frac{ \frac{\partial J}{\partial \vec{\theta}}}{ \frac{\partial^2 J}{\partial \vec{\theta}^2}} \propto \mbox{units of }\, \vec{\theta} \end{align*}
Adadelta: get everything right
\begin{align*} \vec{g}_t & = \nabla_{\theta} \prob{J}{\vec{\theta}} \\ \Delta\vec{\theta}_{t-1} & = \frac{\eta}{\sqrt{{\prob{diag}{\prob{E}{\vec{g}^2}_{t-1}} + \epsilon}}} \\ \prob{E}{\Delta\vec{\theta}^2}_{t-1} & = \gamma\prob{E}{\Delta\vec{\theta}^2}_{t-2} + (1-\gamma)\Delta\vec{\theta}^2_{t-1}\\ \prob{E}{\vec{g}^2}_t & = \gamma\prob{E}{\vec{g}^2}_{t-1} + (1-\gamma)\vec{g}_t^2\\ \vec{\theta} &= \vec{\theta} - \frac{{\sqrt{{\prob{diag}{\prob{E}{\Delta\vec{\theta}^2}_{t-1}} + \epsilon}}} }{{\sqrt{{\prob{diag}{\prob{E}{\vec{g}^2}_{t}} + \epsilon}}} }\vec{g}_t \\ \end{align*}
Adam (adaptive moment)
\begin{align*} \vec{m}_t & = \beta_1 \vec{m}_{t-1} + (1 - \beta_1) \nabla_{\theta} \prob{J}{\theta}\\ \vec{v}_t & = \beta_2 \vec{v}_{t-1} + (1 - \beta_2) (\nabla_{\theta} \prob{J}{\theta})^2\\ \hat{\vec{m}}_t &= \frac{\vec{m}_t}{1 - \beta_1^t}\\ \hat{\vec{v}}_t &= \frac{\vec{v}_t}{1 - \beta_2^t}\\ \vec{\theta}_{t+1} &= \vec{\theta}_t - \frac{\eta}{\sqrt{\hat{\vec{v}}_t} + \epsilon} \hat{\vec{m}}_t\\ \beta_1 &\simeq 0.9 \quad \beta_2 \simeq 0.999 \quad \epsilon \simeq 10^{-8} \end{align*}
Many more
- AdaMax
- Nadam
- AMSgrad
- AdamW
- QHAdam
- AggMo
but use Adam if in doubt
Momentum?
The rise of the SGD

