Advanced Machine Learning

10: Logistic Regression

Outline for the lecture

  • Naïve Bayes recap
  • Defining Logistic Regression
  • Solving Logistic Regression

Naïve Bayes (recap)

Properties and assumptions

Features $X_i$ and $X_j$ are conditionally independent given the class label $Y$
$\prob{P}{X_i,X_j|Y} = \prob{P}{X_i|Y}\prob{P}{X_j|Y}$
$\prob{P}{X_1,\dots, X_d|Y} = \prod_{i=1}^d \prob{P}{X_i|Y}$
$f_{NB}(\vec{x}) = \underset{y}{\argmax} \prod_{i=1}^d \prob{P}{x_i|y}\prob{P}{y}$
Assume a parametric form for $\prob{P}{X_j|Y}$ and $\prob{P}{Y}$
Estimate MLE parameters for these functions.
Plug in and operate the NB classifier

Gaussian Naïve Bayes

$Y \sim \mbox{Bernoulli}(\pi)$ $\prob{P}{X_i = \vec{x}_i|Y = y_k} = \frac{1}{\sigma_{ik}\sqrt{2\pi}} e^{-\frac{(\vec{x}_i - \mu_{ik})^2}{2\sigma_{ik}^2}}$
Different mean and variance for each class $k$ and each pixel $i$.$^*$
Let's assume variance is independent of class: $\sigma_{ik} = \sigma_{i}$

Gaussian NB as a linear classifier

$\prob{P}{X_i = \vec{x}_i|Y = y_k} = \frac{1}{\sigma_{ik}\sqrt{2\pi}} e^{-\frac{(\vec{x}_i - \mu_{ik})^2}{2\sigma_{ik}^2}}$
  • For simplicity consider 2 class problem $\sigma_{i,0} = \sigma_{i, 1}$
  • Decision boundary:
    $\prod_{i=1}^d \prob{P}{x_i|y=0}\prob{P}{y=0} = \prod_{i=1}^d \prob{P}{x_i|y=1}\prob{P}{y=1}$
  • Equivalently:
    $\log\frac{\prod_{i=1}^d \prob{P}{x_i|y=0}\prob{P}{y=0}}{\prod_{i=1}^d \prob{P}{x_i|y=1}\prob{P}{y=1}} = 0$ $\log\frac{\prod_{i=1}^d \prob{P}{x_i|y=0}\prob{P}{y=0}}{\prod_{i=1}^d \prob{P}{x_i|y=1}\prob{P}{y=1}}= \log\frac{1 - \pi}{\pi} +\sum_{i=1}^d \log\frac{\prob{P}{x_i|y=0}}{\prob{P}{x_i|y=1}}$

Gaussian NB as a linear classifier

  • Decision boundary:
    $\log\frac{\prod_{i=1}^d \prob{P}{x_i|y=0}\prob{P}{y=0}}{\prod_{i=1}^d \prob{P}{x_i|y=1}\prob{P}{y=1}} = 0$ $\log\frac{\prod_{i=1}^d \prob{P}{x_i|y=0}\prob{P}{y=0}}{\prod_{i=1}^d \prob{P}{x_i|y=1}\prob{P}{y=1}}= \log\frac{1 - \pi}{\pi} +\sum_{i=1}^d \log\frac{\prob{P}{x_i|y=0}}{\prob{P}{x_i|y=1}}$
  • If you do the algebra:
    $\log\frac{1 - \pi}{\pi} +\sum_{i=1}^d \frac{\mu^2_{i,1} - \mu^2_{i,0}}{2\sigma_i^2} + \sum_{i=1}^d \frac{\mu_{i,1} - \mu_{i,0}}{2\sigma_i^2} x_i = w_0 + \sum_{i=1}^d w_i x_i$

Generative vs. Discriminative

  • Generative classifiers (such as Naïve Bayes)
    • Assume a functional form for $\prob{P}{x,y}$ (or $\prob{P}{x|y}$ and $\prob{P}{y}$)
    • Estimate parameters of $\prob{P}{x|y}$ and $\prob{P}{y}$ from training data
    • Able to generate samples from a trained model
  • Note:
    $\underset{y}{\argmax} \prob{P}{x|y}\prob{P}{y} = \underset{y}{\argmax} \prob{P}{y|x}$
  • Let's learn $\prob{P}{y|x}$ directly!
  • Or learn the decision boundary directly

Defining Logistic regression

And the winner is...

LR poly
according to an autoML tool: polyssifier

Example

loan prediction
from Brandon Foltz

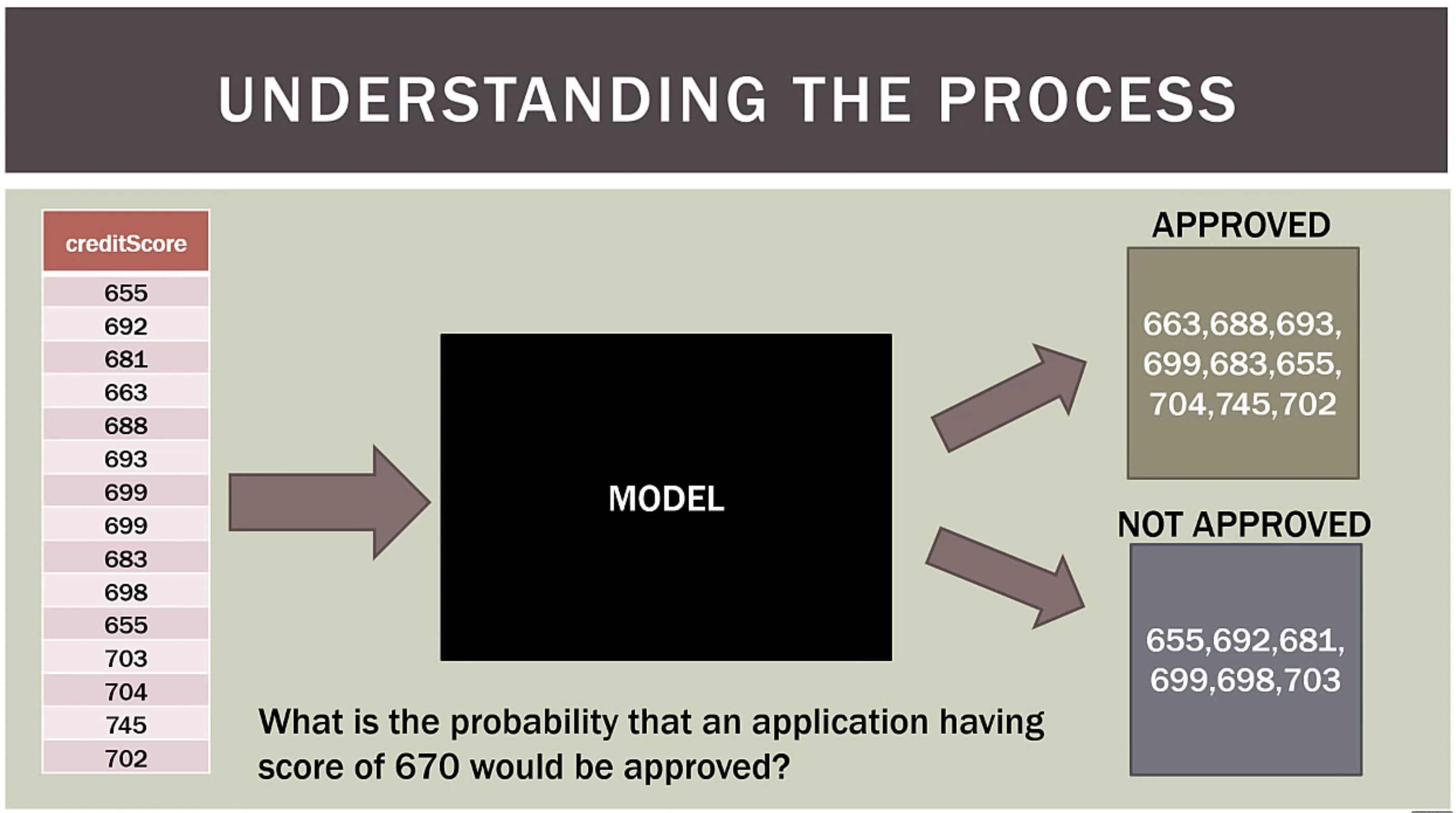
Problem definition

Logistic regression seeks to
  • Model the probability of an event occuring depending on the values of the independent variables, which can be categorical or numerical
  • Estimate the probability that an event occurs for a randomly selected observation versus the probability that the event does not occur
  • Predict the effect of a series of variables on a binary response variable
  • Classify observations by estimating the probability that an observation is in a particular category (e.g. approved or not approved for a loan)
from Brandon Foltz

Our data in 1D

Cox
Sir David Cox

Why not SVM?

Marty 1955
Leyden Jar
for further examples cf. T. Kuhn "The Structure of Scientific Revolutions"

Odds

Probability Corresponding odds
0.5 50:50 or 1
0.9 90:10 or 9
0.999 999:1 or 999
0.01 1:99 or 0.0101
0.001 1:999 or 0.001001

Log-Odds

Log-odds Probability
0 0.5
2.19 0.9
6.9 0.999
-4.6 0.01
-6.9 0.001

Linear Fit to Log-Odds

\begin{array}{ll} \log\left(\frac{p_+}{1-p_+}\right) &= kx + b\\ &= w_1 x + w_0 \\ &= \vec{w}^T\vec{x} \\ \end{array}
\begin{array}{ll} \log\left(\frac{\prob{P}{G=1|X=x}}{\prob{P}{G=K|X=x}}\right) &= \vec{w}_1^T\vec{x}\\ \log\left(\frac{\prob{P}{G=2|X=x}}{\prob{P}{G=K|X=x}}\right) &= \vec{w}_2^T\vec{x}\\ &\vdots \\ \log\left(\frac{\prob{P}{G=K-1|X=x}}{\prob{P}{G=K|X=x}}\right) &= \vec{w}_{K-1}^T\vec{x}\\ \end{array}

What's the probability?

  • $\log\left(\frac{p_+}{1-p_+}\right) = \vec{w}^T\vec{x}$
  • $\frac{p_+}{1-p_+} = e^{\vec{w}^T\vec{x}}$
  • $p_+ = e^{\vec{w}^T\vec{x}}(1-p_+)$
  • $p_+ = e^{\vec{w}^T\vec{x}}-p_+e^{\vec{w}^T\vec{x}}$
  • $p_++p_+e^{\vec{w}^T\vec{x}} = e^{\vec{w}^T\vec{x}}$
  • $p_+(1+e^{\vec{w}^T\vec{x}}) = e^{\vec{w}^T\vec{x}}$
  • $p_+ = \frac{e^{\vec{w}^T\vec{x}}}{1+e^{\vec{w}^T\vec{x}}}$
  • $p_+ = \frac{1}{1+e^{-\vec{w}^T\vec{x}}}$
logistic curve

What's the probability when it is interesting?

  • $\prob{P}{G=k|X=x} = \frac{e^{\vec{w}_k^T\vec{x}}}{1+\sum_i^{K-1}e^{\vec{w}_i^T\vec{x}}}, k = 1, \dots, K-1$
  • $\prob{P}{G=K|X=x} = \frac{1}{1+\sum_i^{K-1}e^{\vec{w}_i^T\vec{x}}}$

Softmax!

\[ \sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \] linear softmax
\[ \sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \]

Softmax!

Laplace0 softmax Laplace1 softmax Laplace2 softmax

Solving Logistic regression

An alternative perspective on log odds

What's posterior probability of class $c_1$ given a sample $\vec{x}$?
\[ \prob{p}{c_1|\vec{x}} = \frac{\prob{p}{\vec{x}|c_1}\prob{p}{c_1}}{\prob{p}{\vec{x}|c_1}\prob{p}{c_1} + \prob{p}{\vec{x}|c_2}\prob{p}{c_2}} \]
Let's introduce $a = \ln\frac{\prob{p}{\vec{x}|c_1}\prob{p}{c_1}}{\prob{p}{\vec{x}|c_2}\prob{p}{c_2}}$
\[ \prob{p}{c_1|\vec{x}} = \frac{1}{1+\exp{(-a)}} = \sigma(a) \]

Logistic Sigmoid

sigmoid
Nice properties of logistic sigmoid \begin{align} \sigma{(-a)} &= 1 - \sigma{(a)}\\ \end{align} $a = \ln{(\frac{\sigma}{1 - \sigma})} \color{#dc322f}{\text{ log odds???}}$
$\frac{d\sigma}{d a} =\sigma(1-\sigma)$

Maximum likelihood estimate

\begin{align} {\cal l}(\vec{w}) &= \underset{\vec{w}}{\argmax} \prod_i^N P_{\vec{w}}(c_k | x_i)\\ {\cal l}(\vec{w}) &= \underset{\vec{w}}{\argmax} \prod_{i:\vec{x}_i \in c_1}^N P_{\vec{w}}(c_1 | x_i)\prod_{i:\vec{x}_i \in c_2}^N P_{\vec{w}}(c_2 | x_i)\\ {\cal l}(\vec{w}) &= \underset{\vec{w}}{\argmax} \prod_{i:\vec{x}_i \in c_1}^N \sigma \prod_{i:\vec{x}_i \in c_2}^N (1 - \sigma)\\ {\cal l}(\vec{w}) &= \underset{\vec{w}}{\argmax} \prod_i^N \sigma_i^{l_1}(1 - \sigma_i)^{1-l_1}\\ \end{align}

Negative Log likelihood

\begin{align} {\cal l}(\vec{w}) &= \underset{\vec{w}}{\argmax} \prod_i^N \sigma_i^{l_1}(1 - \sigma_i)^{1-l_1}\\ \ell(\vec{w}) &= - \sum_i^N ({l_i}\ln(\sigma_i) + (1-l_i)\ln(1 - \sigma_i))\\ \end{align}

Cross Entropy (recap)

\[ H_{p,q} = -\sum_{i=1}^n p_X(x_i) \log q_X(x_i) \]

Negative Log likelihood: How to solve for $\vec{w}$?

\begin{align} \ell(\vec{w}) &= - \sum_i^N ({l_i}\ln(\sigma_i) + (1-l_i)\ln(1 - \sigma_i))\\ \nabla_{\vec{w}} \ell &= \sum_i^N (\sigma_i - l_i)\vec{x}_i\\ \nabla_{\vec{w}} \ell &= {\bf X}^T (\vec{\sigma} - \vec{l}) \stackrel{\text{set}}{=} 0\\ \end{align}

Taylor expansion

\[ f(x) = f(a)+\frac {f^\prime(a)}{1!} (x-a)+ \frac{f''(a)}{2!} (x-a)^2+ \cdots \] \[ f(x) = \sum_{n=0} ^ {\infty} \frac {f^{(n)}(a)}{n!} (x-a)^{n} \]

Taylor expansion

Taylor

Newton-Raphson method

\begin{align} \ell(\vec{w} + \Delta) & = \ell(\vec{w}) + \ell^{\prime}(\vec{w})\Delta + \frac{1}{2}\ell^{\prime\prime}(\vec{w})\Delta^2\\ \frac{\partial \ell(\vec{w} + \Delta)}{\partial \Delta} & \stackrel{set}{=} 0 \\ \ell^{\prime}(\vec{w}) + \ell^{\prime\prime}(\vec{w})\Delta &= 0\\ \Delta &= - \frac{\ell^{\prime}(\vec{w})}{\ell^{\prime\prime}(\vec{w})}\\ \vec{w}_{new} & = \vec{w}_{old} + \Delta = \vec{w}_{old}- \frac{\ell^{\prime}(\vec{w})}{\ell^{\prime\prime}(\vec{w})}\\ \vec{w}_{new} & = \vec{w}_{old} - {\bf H}^{-1}\nabla_\vec{w}\ell \end{align}

Hessian

\[ \mathbf H = \begin{bmatrix} \dfrac{\partial^2 f}{\partial w_1^2} & \dfrac{\partial^2 f}{\partial w_1\,\partial w_2} & \cdots & \dfrac{\partial^2 f}{\partial w_1\,\partial w_n} \\[2.2ex] \dfrac{\partial^2 f}{\partial w_2\,\partial w_1} & \dfrac{\partial^2 f}{\partial w_2^2} & \cdots & \dfrac{\partial^2 f}{\partial w_2\,\partial w_n} \\[2.2ex] \vdots & \vdots & \ddots & \vdots \\[2.2ex] \dfrac{\partial^2 f}{\partial w_n\,\partial w_1} & \dfrac{\partial^2 f}{\partial w_n\,\partial w_2} & \cdots & \dfrac{\partial^2 f}{\partial w_n^2} \end{bmatrix} \]

Newton-Raphson update for linear regression

$f(\vec{w}) = \sum_{i}^{n} (\vec{w}^T\vec{x}_i - y_i)^2$
Let us write in matrix form:
$f(\vec{w}) = (\bf{X}\vec{w} - \vec{y})^T(\bf{X}\vec{w} - \vec{y})$
The gradient:
$\nabla_\vec{w}f = \bf{X}^T\bf{X}\vec{w} - \bf{X}^T\vec{y}$
The Hessian:
$\nabla^2_\vec{w}f = \bf{X}^T\bf{X}$
$\vec{w}_{new} = \vec{w}_{old} - (\bf{X}^T\bf{X})^{-1}(\bf{X}^T\bf{X}\vec{w}_{old} - \bf{X}^T\vec{y})$
$\vec{w}_{new} = \vec{w}_{old} - \vec{w}_{old} + (\bf{X}^T\bf{X})^{-1}\bf{X}^T\vec{y}$
$\vec{w}_{new} = (\bf{X}^T\bf{X})^{-1}\bf{X}^T\vec{y}$

Newton-Raphson update for logistic regression

  • $\nabla_{\vec{w}} \ell = {\bf X}^T (\vec{\sigma} - \vec{l})$
  • ${\bf H} = \nabla\nabla_{\vec{w}} \ell = {\bf X}^T{\bf W}{\bf X}$
  • ${\bf W}_{i,i} = \sigma_i(1-\sigma_i)$
  • $\vec{w}_{new} = \vec{w}_{old} - (\bf{X}^T\bf{W}\bf{X})^{-1}\bf{X}^T(\vec{\sigma} - \vec{l})$
  • bring $(\bf{X}^T\bf{W}\bf{X})^{-1}$ out
  • $\vec{w}_{new} = (\bf{X}^T\bf{W}\bf{X})^{-1}(\bf{X}^T\bf{W}\bf{X}\vec{w}_{old} - \bf{X}^T(\vec{\sigma} - \vec{l}))$
  • $\vec{z} = \bf{X}\vec{w}_{old} - \bf{W}^{-1}(\vec{\sigma} - \vec{l})$
  • $\vec{w}_{new} = (\bf{X}^T\bf{W}\bf{X})^{-1}\bf{X}^T\bf{W}\vec{z}$