Advanced Machine Learning

10: Naive Bayes

Schedule

# date topic description
1 22-Aug-2022 Introduction
2 24-Aug-2022 Foundations of learning
3 29-Aug-2022 PAC learnability
4 31-Aug-2022 Linear algebra (recap) hw1 released
05-Sep-2022 Holiday
5 07-Sep-2022 Linear learning models
6 12-Sep-2022 Principal Component Analysis project ideas
7 14-Sep-2022 Curse of Dimensionality hw1 due
8 19-Sep-2022 Bayesian Decision Theory hw2 release
9 21-Sep-2022 Parameter estimation: MLE
10 26-Sep-2022 Parameter estimation: MAP & NBfinalize teams
11 28-Sep-2022 Logistic Regression
12 03-Oct-2022 Kernel Density Estimation
13 05-Oct-2022 Support Vector Machines hw3, hw2 due
10-Oct-2022 * Mid-point projects checkpoint *
12-Oct-2022 * Midterm: Semester Midpoint exam
14 17-Oct-2022 Matrix Factorization
15 19-Oct-2022 Stochastic Gradient Descent
# date topic description
16 24-Oct-2022 k-means clustering
17 26-Oct-2022 Expectation Maximization hw4, hw3 due
18 31-Oct-2022 Automatic Differentiation
19 02-Nov-2022 Nonlinear embedding approaches
20 07-Nov-2022 Model comparison I
21 09-Nov-2022 Model comparison II hw5, hw4 due
22 14-Nov-2022 Model Calibration
23 16-Nov-2022 Convolutional Neural Networks
21-Nov-2022 Fall break
23-Nov-2022 Fall break
24 28-Nov-2022 Word Embedding hw5 due
30-Nov-2022 Presentation and exam prep day
02-Dec-2022 * Project Final Presentations *
07-Dec-2022 * Project Final Presentations *
12-Dec-2022 * Final Exam *
15-Dec-2022 Grades due

Outline for the lecture

  • MAP Estimation
  • The Naive Bayes Classifier

MAP estimation

I suspect the coin is biased
flipping

What about the knowledge we already have?

We know the coin is “close” to 50-50. What can we do now?
Follow the Bayesian way ...
Rather than estimating a single $\theta$, obtain a distribution over possible values of $\theta$
priors

Prior distribution

What kind of prior distribution do we want to use?
  • Represents expert knowledge (philosophical approach)
  • Simple posterior form (engineering approach)
Uninformative priors:
  • Uniform distribution
uniform prior
Conjugate priors:
  • Closed-form representation of posterior
  • $\prob{P}{\theta}$ and $\prob{P}{\theta|{\cal D}}$ have the same form

Bayes rule (revisited)

Bayes
Bayes, Thomas (1763): An essay towards solving a problem in the doctrine of chances. Philosophical Transactions of the Royal Society of London, 53:370-418
It is on the homework

Chain Rule & Bayes rule

Chain rule:
$\prob{P}{X,Y} = \prob{P}{X|Y}\prob{P}{Y} = \prob{P}{Y|X}\prob{P}{X}$
Bayes rule:
$\prob{P}{X|Y} = \frac{\prob{P}{Y|X}\prob{P}{X}}{\prob{P}{Y}}$
Bayes rule is important for reverse conditioning

Bayesian Learning

  • Use Bayes rule
    $ \prob{P}{\theta|{\cal D}} = \frac{\prob{P}{{\cal D}|\theta}\prob{P}{\theta}}{\prob{P}{\vec{{\cal D}}}} $
  • Or equivalently
    $ \prob{P}{\theta|{\cal D}} \propto \prob{P}{{\cal D}|\theta}\prob{P}{\theta} $
  • Which is, as we know:
    $ \mbox{posterior} \propto \mbox{likelihood}\times\mbox{prior} $

    • MLE vs. MAP

    • Maximum Likelihood estimation (MLE)
      Choose value that maximizes the probability of observed data
      $ \hat{\theta}_{MLE} = \underset{\theta}{\argmax} \prob{P}{{\cal D}|\theta} $
    • Maximum a posteriori (MAP) estimation Choose value that is most probable given observed data and prior belief \begin{align} \hat{\theta}_{MAP} & = \underset{\theta}{\argmax} \prob{P}{\theta|{\cal D}}\\ & = \underset{\theta}{\argmax} \prob{P}{{\cal D}|\theta}\prob{P}{\theta} \end{align}

    MAP for Binomial distribution

    Coin flip problem: Binomial likelihood
    $\prob{P}{{\cal D}|\theta} = {n \choose \alpha_H} \theta^{\alpha_H} (1-\theta)^{\alpha_T}$
    If the prior is Beta distribution,
    \begin{align} \prob{P}{\theta} &= \frac{1}{\prob{B}{\beta_H,\beta_T}} \theta^{\beta_H-1}(1-\theta)^{\beta_T-1} \sim \prob{Beta}{\beta_H,\beta_T}\\ \prob{B}{x,y} &= \int_0^1 t^{x-1}(1-t)^{y-1}dt = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)} \end{align}
    posterior is Beta distribution

    MAP for Binomial distribution

    Binomial likelihood
    $\prob{P}{{\cal D}|\theta} = {n \choose \alpha_H} \theta^{\alpha_H} (1-\theta)^{\alpha_T}$
    Beta prior
    $ \prob{P}{\theta} \sim \prob{Beta}{\beta_H,\beta_T} $
    Beta posterior
    $\prob{P}{\theta|{\cal D}} = \prob{Beta}{\beta_H+\alpha_H, \beta_T + \alpha_T}$
    $\prob{P}{\theta}$ and $\prob{P}{\theta|{\cal D}}$ have the same form: Conjugate prior
    $\hat{\theta}_{MAP} = \frac{\alpha_H+\beta_H -1}{\alpha_H + \beta_H + \alpha_T + \beta_T -2}$

    Beta distribution

    More concentrated as values of $\alpha, \beta$ increase
    beta

    Beta conjugate prior

    $\prob{P}{\theta} \sim \prob{Beta}{\beta_H,\beta_T}$ $\prob{P}{\theta|{\cal D}} = \prob{Beta}{\beta_H+\alpha_H, \beta_T + \alpha_T}$
    beta
    $n = \alpha_H + \alpha_T$ increases $\rightarrow$
    As we get more samples, effect of prior “washes out”
    dice

    Multinomial distribution

    Example: Dice roll problem (6 outcomes instead of 2)
    • Likelihood is $\sim \prob{Multinomial}{\theta=\{\theta_1,\theta_2,\dots,\theta_k\}}$
      $ \prob{P}{{\cal D}|\theta} = \theta^{\alpha_1}_1\theta^{\alpha_2}_2,\dots,\theta^{\alpha_k}_k $
    • If prior is the Dirichlet distribution:
      $ \prob{P}{\theta} = \frac{\prod_{i=1}^k\theta_i^{\beta_i-1}}{\prob{B}{\beta_1, \beta_2, \dots, \beta_k}} $
    • the posterior is the Dirichlet distribution:
      \[ \prob{P}{\theta|{\cal D}} = \prob{Dirichlet}{\beta_1+\alpha_1, \dots, \beta_k+\alpha_k} \]

    Bayes rule (practice again)

    Fruits in boxes (homework)

    boxes

    AIDS test

    Data
    • Approximately 0.1% are infected
    • Test detects all infections (no false negatives)
    • Test reports positive for 1% of healthy
    • $+$ - tested positively
    • $\prob{P}{AIDS} = 0.001$
    • $\prob{P}{\overline{AIDS}} = 0.999$
    • $\prob{P}{+|AIDS} = 1$
    • $\prob{P}{+|\overline{AIDS}} = 0.01$
    • $\prob{P}{AIDS|+} \approx 9\%$
    \begin{align} \prob{P}{+} & = \prob{P}{+|AIDS}\prob{P}{AIDS}\\ & + \prob{P}{+|\overline{AIDS}}\prob{P}{\overline{AIDS}}\\ \prob{P}{AIDS|+} &= \frac{\prob{P}{+|AIDS}\prob{P}{AIDS}}{\prob{P}{+}} \end{align}

    Improve the diagnosis

    Use a follow-up test!
    • Test 2 reports positive for 90% of infected
    • Test 2 reports positive for 5% of healthy people
    • $+_1, +_2$ - tested positively
    • $\prob{P}{AIDS} = 0.001$
    • $\prob{P}{\overline{AIDS}} = 0.999$
    • $\prob{P}{+_1,+_2|AIDS}$
    • $\prob{P}{+_1, +_2|\overline{AIDS}}$
    • $\prob{P}{AIDS|+_1, +_2} \approx 64%\%$
    \begin{align} \prob{P}{+_1,+_2} & = \prob{P}{+_1,+_2|AIDS}\prob{P}{AIDS}\\ & + \prob{P}{+_1,+_2|\overline{AIDS}}\prob{P}{\overline{AIDS}}\\ \prob{P}{AIDS|+_1, +_2} &= \frac{\prob{P}{+_1,+_2|AIDS}\prob{P}{AIDS}}{\prob{P}{+_1,+_2}} \end{align}
    • Outcomes are not independent but test 1 and 2 are conditionally independent $\prob{P}{t_1,t_2|a} = \prob{P}{t_1|a} \prob{P}{t_2|a}$

    The Naïve Bayes Classifier

    spam

    Detector for spam filtering

    • date
    • time
    • recipient path
    • IP number
    • sender
    • encoding
    • many more features
    email

    The Naïve Bayes Assumptions

    Features $X_i$ and $X_j$ are conditionally independent given the class label $Y$
    $\prob{P}{X_i,X_j|Y} = \prob{P}{X_i|Y}\prob{P}{X_j|Y}$
    $\prob{P}{X_1,\dots, X_d|Y} = \prod_{i=1}^d \prob{P}{X_i|Y}$
    How many parameters to estimate?
    $\mathbf{X}$ is a binary vector where each position encodes presence or absence of a feature. $\mathbf{Y}$ has K classes.
    $(2^d - 1)K$ vs. $(2-1)dK$

    The Naïve Bayes Classifier

    Given:
    • Class prior $\prob{P}{Y}$
    • $d$ conditionally independent features $X_1, X_2, \dots, X_d$ given the class label $Y$
    • For each $X_i$, we have the conditional likelihood $\prob{P}{X_i|Y}$
    Decision rule: \begin{align} f_{NB}(\vec{x}) &= \underset{y}{\argmax} \prob{P}{x_1,\dots,x_d|y}\prob{P}{y} \\ &= \underset{y}{\argmax} \prod_{i=1}^d \prob{P}{x_i|y}\prob{P}{y}\\ \end{align}

    The Naïve Bayes for discrete features

    Training data: $\{(\vec{x}^j,y^j)\}_{j=1}^n \vec{x}^j = (x_1^j, \dots, x_d^j)$
    $n$ d-dimensional features plus class labels
    $f_{NB}(\vec{x}) = \underset{y}{\argmax} \prod_{i=1}^d \prob{P}{x_i|y}\prob{P}{y}$
    Estimate probabilities with relative frequencies!
    • For class prior $\prob{P}{y} = \frac{\{\#j:y^j = y\}}{n}$
    • For likelihood $\frac{\prob{P}{x_i,y}}{\prob{P}{y}} = \frac{\{\#j:\vec{x}_i^j = x_i, y^j=y\}/n}{\{\#j:y^j = y\}/n}$

    Text Classification

    • Ex1. Classify e-mails: $y \in \{ \mbox{Spam}, \mbox{NotSpam} \}$
    • Ex2. Classify articles into topics
    • What are the features of $\mathbf{X}$?
    • Full text!

    Text Classification: naïvely

    • Fix max_len of an article and encode positions $\mathbf{X} = \{X_1, \dots, X_{1000}\}$
    • $X_i$ is a word at $i^{th}$ position. $X_i \in \{0, \dots, D\}$, where $D$ is the size of the vocabulary (say 50,000 words).
    • $\prob{P}{\mathbf{X}|Y}$ is large
    • Need to estimate $K D^{1000} = K 50000^{1000}$ parameters
    Naive Bayes to the rescue!
    • $\prob{P}{X_i^j|y}$ probability of word $j$ at position $i$ for class $y$
    • Need to estimate $DK1000 = 50000K1000$ parameters
    bow

    Text Classification: bag of words

    Word order and positions do not matter! Only presence
    • $D=2 \implies$ $X_i$ is binary again
    • $\mathbf{X}$ is vocabulary-length (say 50000) binary vector.
    • Need to estimate $DK50000 = 50000K$ parameters
    Works really well in practice!
    An empirical study of the naive Bayes classifier

    Insufficient training data

    • What if you never see $x_i = v$ for $y = k$?
    • No word "Luxury", when $y = \mbox{NoSpam}$ in the dataset
      $\prob{P}{\mbox{Luxury} = 1, \mbox{NoSpam}} = 0 \implies \prob{P}{\mbox{Luxury} = 1| \mbox{NoSpam}} = 0$
    • $\prob{P}{\mbox{Luxury}=1, X_2, \dots, X_n| Y} = $
    • $\prob{P}{\mbox{Luxury}=1| Y} \prod_{i=2}^n \prob{P}{X_i|Y} =$
    • $0$
    • Now what?

    The Naïve Bayes Properties

    • The counts seemed confusing but it is just a consequence of our choice of the likelihood and prior
    • Conveniently estimated everything relative to individual points
    • Need to watch out for empty label-feature combinations in the data
    • Need to evaluate log probabilities, as products of small numbers lead to problems

    What if the features are continuous?

    Character recognition: $\vec{x}_{ij}$ is intensity at pixel $(i,j)$
    mnist
    Gaussian Naïve Bayes
    $\prob{P}{X_i = \vec{x}_i|Y = y_k} = \frac{1}{\sigma_{ik}\sqrt{2\pi}} e^{-\frac{(\vec{x}_i - \mu_{ik})^2}{2\sigma_{ik^2}}}$
    Different mean and variance for each class $k$ and each pixel $i$.$^*$
    Sometimes we can assume that variance is independent of $Y \rightarrow \sigma_i$, or $X_i \rightarrow \sigma_k$ or both $\sigma$

    Example: classifying mental states

    • resolution around $1^3$ mm
    • 1 image per 2 seconds
    • about $15,000$ voxels per "frame"
    • non-invasive and safe
    • measures Blood Oxygenation Level Dependent (BOLD) response
    MRI
    Learning to Decode Cognitive States from Brain Images

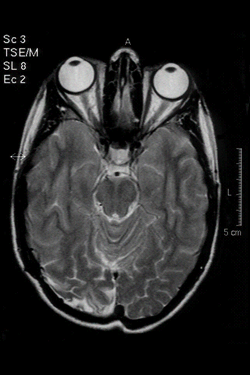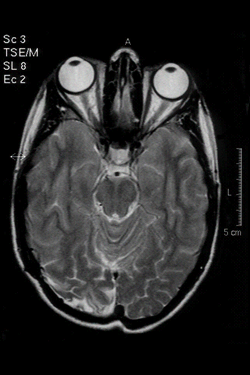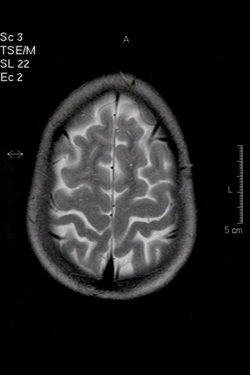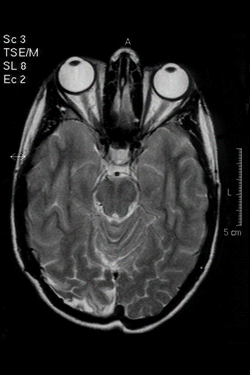
    P(Brain Activity | Word Category)

    Pairwise classification accuracy $78-99\%$ on 12 participants
    Mitchell
    Learning to Decode Cognitive States from Brain Images