Advanced Machine Learning

09: Maximum Likelihood Estimation

Schedule (you are here )

#	date	topic	description
1	25-Aug-2025	Introduction
2	27-Aug-2025	Foundations of learning	Drop/Add
3	01-Sep-2025	Labor Day Holiday	Holiday
4	03-Sep-2025	Linear algebra (self-recap)	HW1
5	08-Sep-2025	PAC learnability
6	10-Sep-2025	Linear learning models
7	15-Sep-2025	Principal Component Analysis	Project ideas
8	17-Sep-2025	Curse of Dimensionality
9	22-Sep-2025	Bayesian Decision Theory	HW2, HW1 due
10	24-Sep-2025	Parameter estimation: MLE
11	29-Sep-2025	Parameter estimation: MAP & NB	finalize teams
12	01-Oct-2025	Logistic Regression
13	06-Oct-2025	Kernel Density Estimation
14	08-Oct-2025	Support Vector Machines	HW3, HW2 due
15	13-Oct-2025	* Midterm	Exam
16	15-Oct-2025	Matrix Factorization
17	20-Oct-2025	* Mid-point projects checkpoint	*
18	22-Oct-2025	k-means clustering

#	date	topic	description
19	27-Oct-2025	Expectation Maximization
20	29-Oct-2025	Stochastic Gradient Descent	HW4, HW3 due
21	03-Nov-2025	Automatic Differentiation
22	05-Nov-2025	Nonlinear embedding approaches
23	10-Nov-2025	Model comparison I
24	12-Nov-2025	Model comparison II	HW5, HW4 due
25	17-Nov-2025	Model Calibration
26	19-Nov-2025	Convolutional Neural Networks
27	24-Nov-2025	Thanksgiving Break	Holiday
28	26-Nov-2025	Thanksgiving Break	Holiday
29	01-Dec-2025	Word Embedding
30	03-Dec-2025	* Project Final Presentations	HW5 due, P
31	08-Dec-2025	Extra prep day	Classes End
32	10-Dec-2025	* Final Exam	Exam
34	17-Dec-2025	Project Reports	due
35	19-Dec-2025	Grades due 5 p.m.

Outline for the lecture

Independence
Parameter estimation: MLE
MLE and KL-divergence

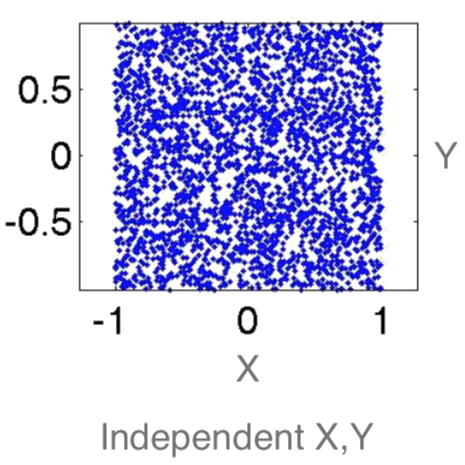
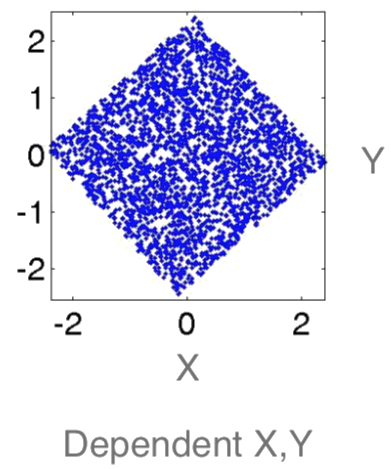
Independence

Independent random variables: \begin{align} \prob{P}{X,Y} &= \prob{P}{X}\prob{P}{Y}\\ \prob{P}{X|Y} &= \prob{P}{X} \end{align}

$Y$ and $X$ don't contain information about each other.
Observing $Y$ does not help predicting $X$.
Observing $X$ does not help predicting $Y$.

Examples:
Independent: winning on roulette this week and next week
Dependent: Russian roulette

inependent/dependent

Conditionally Independent

Conditionally independent:
$$\prob{P}{X,Y|Z} = \prob{P}{X|Z}\prob{P}{Y|Z}$$ Knowing $Z$ makes $X$ and $Y$ independent

Examples:
Dependent: shoe size and reading skills in kids
Conditionally Independent: shoe size and readnig skills given age

Storks deliver babies: Highly statistically significant correlation ($p=0.008$) exists between stork populations and human birth rates across Europe

Conditionally Independent

London taxi drivers: A survey has pointed out a positive and significant correlation between the number of accidents and wearing coats. They concluded that coats could hinder movements of drivers and be the cause of accidents. A new law was prepared to prohibit drivers from wearing coats when driving.

Finally another study pointed out that people wear coats when it rains...

Correlation $\ne$ Causation

Parameter estimation: MLE

a machine learning problem

Estimating probabilities

Flipping a coin

I have a coin, if I flip it, what's the probability it will fall with head up?

Let us flip it a few times to estimate the probability: a flip

The estimated probability is $\frac{3}{5}$. "Frequency of heads"

Flipping a coin

The estimated probability is $\frac{3}{5}$. "Frequency of heads"

Why frequency of heads???
How good is this estimation???
Why is this a machine learning problem???

Let's go ahead and answer these questions

QUESTION 1: Why frequency of heads???

Frequency of heads is exactly the maximum likelihood estimator (MLE) for this problem
MLE has nice properties
and bad ones too, but that's another story

Maximum Likelihood Estimation

MLE for Bernoulli distribution

Data $D = $ $D = \{x_i\}_{i=1}^n, x_i \in \{\text{H}, \text{T}\}$

$\prob{P}{\text{Heads}} = \theta, \prob{P}{\text{Tails}} = 1-\theta$

Flips are i.i.d.:

Independent events
Identically distributed according to Bernoulli distribution

MLE: Choose $\theta$ that maximizes the probability of observed data

Maximum Likelihood Estimation

MLE: Choose $\theta$ that maximizes the probability of observed data

\begin{align} \hat{\theta}_{MLE} &\fragment{1}{ = \underset{\theta}{\argmax} \prob{P}{D|\theta}}\\ &\fragment{2}{ = \underset{\theta}{\argmax} \displaystyle{\prod_{i=1}^n}\prob{P}{x_i|\theta} \color{#dc322f}{\text{ independent draws}}}\\ &\fragment{3}{ = \underset{\theta}{\argmax} \displaystyle{\prod_{i:x_i=H}^{\alpha_H}}\theta \displaystyle{\prod_{j:x_j=T}^{\alpha_T}}(1-\theta) \color{#dc322f}{\stackrel{\text{identically}}{\text{distributed}}}}\\ &\fragment{4}{ = \underset{\theta}{\argmax} \theta^{\alpha_H} (1-\theta)^{\alpha_T}}\\ \end{align}

$J(\theta) = \theta^{\alpha_H} (1-\theta)^{\alpha_T}$

MLE: Choose $\theta$ that maximizes the probability of observed data

\begin{align} \hat{\theta}_{MLE} & = \underset{\theta}{\argmax} \prob{P}{D|\theta}\\ J(\theta) & = \theta^{\alpha_H} (1-\theta)^{\alpha_T}\\ \frac{\partial J(\theta)}{\partial \theta} &= \alpha_H \theta^{\alpha_H-1} (1-\theta)^{\alpha_T} - \alpha_T \theta^{\alpha_H} (1-\theta)^{\alpha_T-1} \stackrel{\text{set}}{=} 0 \end{align} \begin{align} (\alpha_H(1 - \theta) - \alpha_T\theta)\theta^{\alpha_h-1}(1-\theta)^{\alpha_T-1} &= 0\\ \alpha_H(1 - \theta) - \alpha_T\theta &= 0\\ \hat{\theta}_{MLE} &= \frac{\alpha_H}{\alpha_H + \alpha_T}\\ \end{align}

That's exactly "Frequency of heads"

Flipping a coin

The estimated probability is $\frac{3}{5}$. "Frequency of heads"

Why frequency of heads???
How good is this estimation???
Why is this a machine learning problem???

Question2: How good is this estimation???

$$ \hat{\theta}_{MLE} = \frac{\alpha_H}{\alpha_H + \alpha_T} $$

How many flips do I need ?

I flipped the coins 5 times: 3 heads, 2 tails $$ \hat{\theta}_{MLE} = \frac{3}{5} $$
What if I flipped 26 heads and 24 tails? $$ \hat{\theta}_{MLE} = \frac{26}{50} $$

Which estimator should we trust more?

Simple bound

Let $\theta^*$ be the true parameter.

For $n = \alpha_H + \alpha_T$, and $\hat{\theta}_{MLE} = \frac{\alpha_H}{\alpha_H + \alpha_T}$

For any $\epsilon \gt 0$:

Hoeffding's inequality:

\begin{align} \prob{P}{|\hat{\theta} - \theta^*| \ge \epsilon} \le 2e^{-2n\epsilon^2} \end{align}

PAC learning

I want to know the coin parameter $\theta$, within $\epsilon = 0.1$ error with probability at least $1-\delta = 0.95$

How many flips do I need?
\begin{align} \prob{P}{|\hat{\theta} - \theta^*| \ge \epsilon} & \le 2e^{-2n\epsilon^2} \le \delta \end{align}
How many samples do I need?
\begin{align} n & \ge \frac{\ln (2/\delta)}{2\epsilon^2} \approx 185 \end{align}

Flipping a coin

The estimated probability is $\frac{3}{5}$. "Frequency of heads"

Why frequency of heads???
How good is this estimation???
Why is this a machine learning problem???

Question2: Why is this an ML problem???

Machine Learning is the study of algorithms that

improve their performance
at some task
with experience

improves: accuracy of the predicted probability
task: predicting the probability of heads
experience: the more flips the better the estimate

What about continuous features?

Let us try Gaussians...

\begin{align} \prob{p}{x|\mu,\sigma} &= \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} = {\cal N}_x(\mu, \sigma) \end{align}

MLE for Gaussian $\mu$ and $\sigma^2$

$\theta = (\mu, \sigma^2)$ that maximizes the probability of observed data \begin{align} \hat{\theta}_{MLE} & = \underset{\theta}{\argmax} \prob{P}{D|\theta}\\ & = \underset{\theta}{\argmax} \displaystyle{\prod_{i=1}^n}\prob{P}{x_i|\theta} \color{#dc322f}{\text{ independent draws}}\\ & = \underset{\theta}{\argmax} \displaystyle{\prod_{i=1}^n} \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_i-\mu)^2}{2\sigma^2}} \color{#dc322f}{\text{ i.i.d}}\\ & = \underset{\theta}{\argmax} \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{\sum_{i=1}^n(x_i-\mu)^2}{2\sigma^2}}\\ \end{align}

Derive $\hat{\mu}_{MLE}$

MLE for Gaussian $\mu$ and $\sigma^2$

\begin{align} \hat{\mu}_{MLE} &= \frac{1}{n} \displaystyle\sum_{i=1}^n x_i\\ \hat{\sigma}^2_{MLE} &= \frac{1}{n} \displaystyle\sum_{i=1}^n (x_i - \hat{\mu}_{MLE})^2\\ \end{align}

MLE for $\sigma^2$ of a Gaussian is biased: expected result of estimation is not the true parameter! $$\hat{\sigma}^2_{unbiased} = \frac{1}{n-1} \displaystyle\sum_{i=1}^n (x_i - \hat{\mu}_{MLE})^2$$

Refresher: Exponential Family

MLE and KL-divergence

How to measure Information

Messages are strings of characters from a fixed alphabet.
The amount of information contained in a message should be a function of the total number of possible messages.
If you have an alphabet with $s$ symbols, then there are $s^\ell$ messages of length, $\ell$.
The amount of information contained in two messages should be the sum of the information contained in the individual messages.
The amount of information in $\ell$ messages of length one should equal the amount of information in one message of length $\ell$.

Hartley's Information (1928)

The only function which satisfies these requirements: \[ \ell \log(s) = \log(s^\ell) \]

Shannon's entropy (1948)

Let $X$ be a discrete random variable with $n$ outcomes, $\{x_1,...,x_n\}$. The probability that the outcome will be $x_i$ is $p(x_i)$. The average information (or entropy) contained in a message about the outcome of $X$ is:

\[ H_p = -\sum_{i=1}^n p_X(x_i) \log p_X(x_i) \]

Cross Entropy

\[ H_{p,q} = -\sum_{i=1}^n p_X(x_i) \log q_X(x_i) \]

Kullback-Leibler (KL) divergence

\[ D_{\rm KL} (P\|Q) = \int P(x) \log \frac{P(x)}{Q(x)} \]

\[ D_{\rm KL} (P\|Q) = \EE_{X\sim P} \left[ \log \frac{P(x)}{Q(x)} \right] \]

\[ D_{\rm KL} (P\|Q) = \EE_{X\sim P} \log P(x) - \EE_{X\sim P} \log Q(x) \]

KL divergence is not symmetric

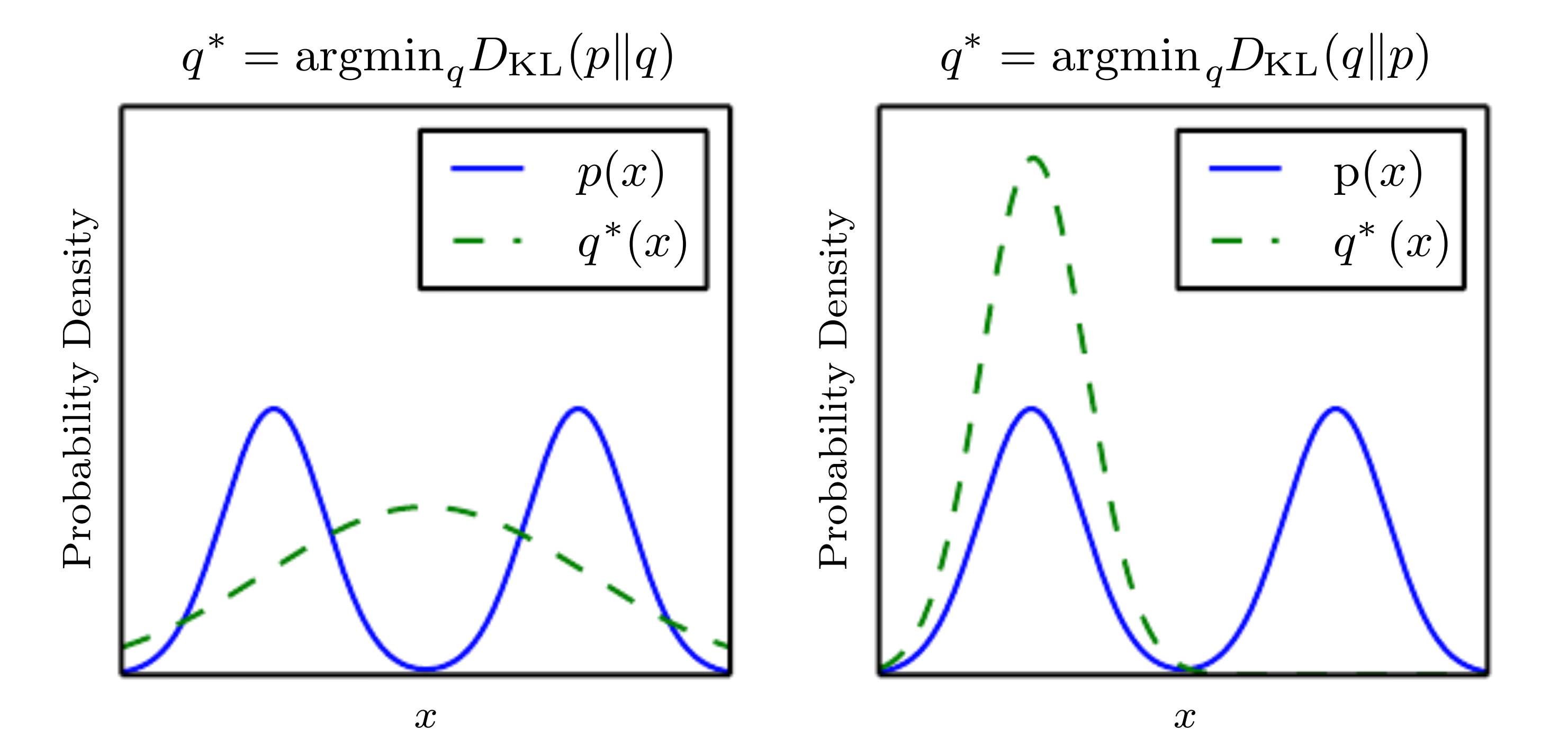https://www.cs.toronto.edu/~duvenaud/distill_bayes_net/public/

MLE is KL-divergence minimization

$ \hat{\theta}_{MLE} = \underset{\theta}{\argmax} \prob{Q}{D|\theta} $
$ \hat{\theta}_{MLE} = \underset{\theta}{\argmax} \prod_{i=1}^{n} \prob{Q}{x_i|\theta} $
$ \hat{\theta}_{MLE} = \underset{\theta}{\argmax} \sum_{i=1}^{n} \log \prob{Q}{x_i|\theta} $
$ \hat{\theta}_{MLE} = \underset{\theta}{\argmax} \EE_{X\sim P} \log \prob{Q}{X|\theta} $
$ D_{\rm KL} (P\|Q) = \EE_{X\sim P} \log P(x) - \EE_{X\sim P} \log Q(x) $