Advanced Machine Learning

07: Curse of Dimensionality

Schedule (you are here )

#	date	topic	description
1	24-Aug-2026	Introduction
2	26-Aug-2026	Foundations of learning	Drop/Add
3	31-Aug-2026	PAC learnability	HW1
4	02-Sep-2026	Linear learning models
5	07-Sep-2026	Labor Day Holiday	Holiday
6	09-Sep-2026	Principal Component Analysis	Project ideas
7	14-Sep-2026	Curse of Dimensionality	HW2, HW1 due
8	16-Sep-2026	Bayesian Decision Theory
9	21-Sep-2026	Parameter estimation: MLE
10	23-Sep-2026	Parameter estimation: MAP & NB	finalize teams
11	28-Sep-2026	Logistic Regression	HW3, HW2 due
12	30-Sep-2026	Kernel Density Estimation
13	05-Oct-2026	Support Vector Machines
14	07-Oct-2026	Matrix Factorization
15	12-Oct-2026	* Midterm	Exam, HW3 due
16	14-Oct-2026	k-means clustering
17	19-Oct-2026	Invited: Intro to Causal Learning I

#	date	topic	description
18	21-Oct-2026	Invited: Intro to Causal Learning II
19	26-Oct-2026	* Mid-point projects checkpoint	HW4, P
20	28-Oct-2026	Expectation Maximization
21	02-Nov-2026	Stochastic Gradient Descent
22	04-Nov-2026	Automatic Differentiation
23	09-Nov-2026	Nonlinear embedding approaches	HW5, HW4 due
24	11-Nov-2026	Model comparison
25	16-Nov-2026	Model Calibration
26	18-Nov-2026	Convolutional Neural Networks
27	23-Nov-2026	Thanksgiving Break	Holiday
28	25-Nov-2026	Thanksgiving Break	Holiday
29	30-Nov-2026	Word Embedding
30	02-Dec-2026	Project Final Presentations	HW5 due, P
31	07-Dec-2026	Presentation spillover / Exam prep	Classes End
32	09-Dec-2026	* Final Exam	Exam
33	16-Dec-2026	Project Reports	due
34	17-Dec-2026	Grades due 5 p.m.	PAWS

Outline of this lecture

Curse of dimensionality

Curse of dimensionality

How much rind?

Step 1/8: Real Watermelon

Dim: D = 1, Rind: ε = 15%

Flesh: (1 − ε)^D = 85.0%

Rind: 1 − (1 − ε)^D = 15.0%

Rind ε: 15%

1. Step 0: Take a watermelon of radius R with a rind of thickness εR (e.g. 15% of radius).
2. Step 1-3 (1D): Cut a cylindrical core plug across the center. The rind occupies 15% of the radius on each end.
3. Step 4-5 (2D): Take a 2D cross-sectional slice. The rind area fraction is 1 - (1 - ε)² = 1 - 0.85² = 27.75% ≈ 28%. Nearly a third of the slice is skin!
4. Step 6 (3D): Consider the full 3D sphere. The rind volume fraction is 1 - (1 - ε)³ = 1 - 0.85³ ≈ 38.6% ≈ 39%. Almost 40% of the entire fruit is rind!
5. Step 7 (High-D): In D dimensions, the fraction of volume in the rind is 1 - (1 - ε)^D. As D grows, (1 - ε)^D rapidly drops to 0, so the rind volume fraction approaches 100%! Even with a razor-thin 2% rind (ε = 0.02), in D = 100, 87% of the melon is rind; in D = 200, over 98% is rind! In high dimensions, almost all the volume of any object is concentrated in a paper-thin surface shell.

Generalized Pythagoras Theorem

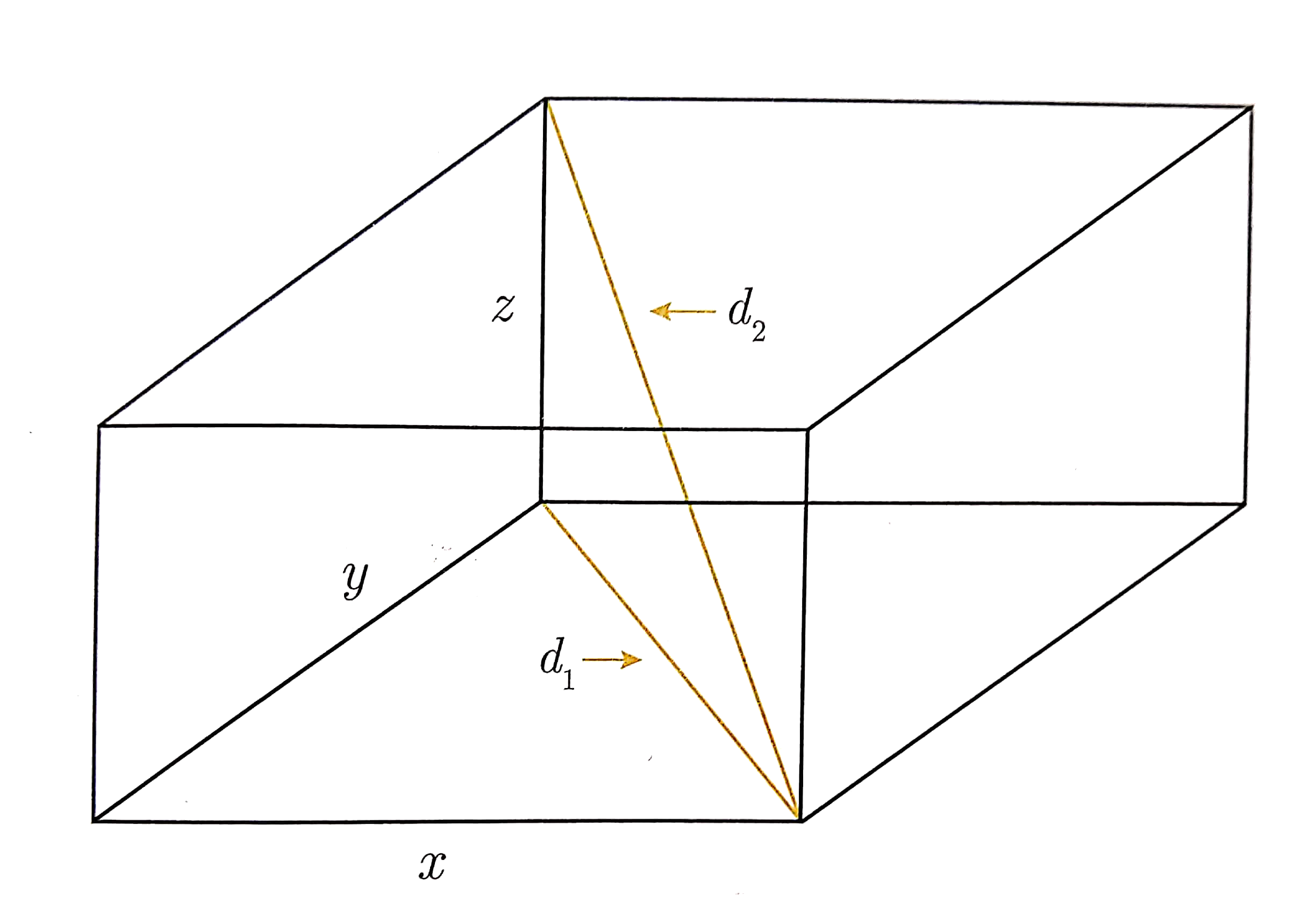$ D^2 = \sum_{i=1}^{n} x^2_{i} $

Trapezoid rule

Stirling approximation for $n!$

$\ln n! = \sum_{k=1}^n \ln k$
$\int_1^n \ln x dx$
$\int_1^n \ln x dx = n\ln n -n +1$
$\int_1^n \ln x dx \sim {1 \over 2}\ln 1 + \ln 2 + \ln 3 + \dots + {1 \over 2}\ln n$
$\sum_{k=1}^n \ln k \sim n\ln n - n + 1 + {1 \over 2}\ln n$
$n! \sim Cn^ne^{-n}\sqrt{n}$
$C = \sqrt{2\pi}$
$n! \sim n^ne^{-n}\sqrt{2\pi n}$

1. Factorial product is difficult to analyze directly, so we work with logarithms: ln(n!) = Σ ln(k).
2. The discrete sum Σ ln(k) is approximated by the integral ∫ ln(x) dx from 1 to n.
3. Integrate by parts: ∫ ln(x) dx = x ln(x) - x |₁ⁿ = n ln(n) - n + 1.
4. Using the trapezoidal numerical quadrature rule: the integral equals (1/2)ln(1) + ln(2) + ... + (1/2)ln(n).
5. Adding (1/2)ln(n) to both sides yields the sum Σ ln(k) ≈ n ln(n) - n + 1 + (1/2)ln(n).
6. Exponentiating both sides yields n! ≈ C * n^n * e^(-n) * √n.
7. The constant C = √(2π) comes from Wallis' product / Gaussian integral.
8. Result: Stirling's famous formula n! ~ √(2πn) (n/e)^n.

Stirling approximation for $n!$

$n$	Stirling	True	Stirling/True
1	0.92214	1	0.92214
2	1.91900	2	0.95950
3	5.83621	6	0.97270
4	23.50618	24	0.97942
5	118.01917	120	0.98349
6	710.07818	720	0.98622
7	4,980.3958	5,040	0.98817
8	39,902.3955	40,320	0.98964
9	359,536.87	362,880	0.99079
10	3,598,695.6	3,628,800	0.99170

$\Gamma$ (Gamma) function

$\Gamma(n) = \displaystyle\int_0^{\infty} x^{n-1}e^{-x}dx$
Integration by parts: $\int udv = uv - \int vdu$
$u=x^{n-1}$, $dv = e^{-x}dx$, $du = (n-1)x^{n-2}dx$, $v = -e^{-x}$
$\Gamma(n) = -e^{-x}x^{n-1} \displaystyle|_0^{\infty} + (n-1)\int_0^{\infty} x^{n-2}e^{-x}dx$
$\Gamma(n) = (n-1)\Gamma(n-1)$
$\Gamma(1) = 1$
$\Gamma(n) = (n - 1)!$

$\Gamma({1 \over 2})$

$\Gamma({1 \over 2}) = \displaystyle\int_0^{\infty} x^{-{1 \over 2}}e^{-x}dx$
Set $x = t^2$, follows $dx = 2tdt$
$\Gamma({1 \over 2}) = 2 \displaystyle\int_0^{\infty} e^{-t^2}dt = \displaystyle\int_{-\infty}^{\infty} e^{-t^2}dt$
$\Gamma^2(\frac{1}{2}) = \displaystyle\int_{-\infty}^{\infty}\displaystyle\int_{-\infty}^{\infty} e^{-(x^2+y^2)dxdy}$
$\Gamma^2(\frac{1}{2}) = \displaystyle\int_{0}^{2\pi}\int_{0}^{\infty} r e^{-r^2} dr d\theta$
$\Gamma^2(\frac{1}{2}) = \pi $
$\Gamma(\frac{1}{2}) = \sqrt{\pi} $

Hypersphere Volume

$\mbox{volume} = C_n r^n$
$C_1 = 2$, $C_2 = \pi$, $C_3 = \frac{4\pi}{3}$
$\mbox{surface area} = \frac{dV_n(r)}{dr} = n C_n r^{n-1}$
$\left(\frac{dV_n(r)}{dr}\right)dr = n C_n r^{n-1}dr$
\begin{align} \Gamma^n\left(\frac{1}{2}\right) = \pi^{n/2} &= \displaystyle \int_0^{\infty} e^{-r^2} \left(\frac{dV_n(r)}{dr}\right)dr \\ & = \frac{nC_n}{2} \displaystyle \int_0^{\infty} e^{-t} t^{n/2-1}dt \\ & = \frac{nC_n}{2} \Gamma\left(\frac{n}{2}\right)\\ & = C_n \Gamma\left(\frac{n}{2} + 1\right) \end{align}

hyperSphere Volume

\begin{align} C_n &= \frac{\pi^{n/2}}{\Gamma(\frac{n}{2} + 1)}\\ C_nr^n & = \frac{(\pi r^2)^k}{k!} \to 0 \\ & \mbox{ as } k\to\infty \end{align}

Dimension $n$	Coefficient $C_n$
1	2	= 2.0000...
2	$\pi$	= 3.14159...
3	$4\pi/3$	= 4.18879...
4	$\pi^2/2$	=4.93480...
5	$8\pi^2/15$	=5.26379...
6	$\pi^3/6$	=5.16771...
7	$16\pi^3/105$	=4.72477...
8	$\pi^4/24$	=4.05871...
9	$32\pi^4/945$	=3.29851...
10	$\pi^5/120$	=2.55016...
$2k$	$\pi^k/k!$	$\to 0$

In a general hyperwatermelonsphere

\begin{align} \frac{C_nr^n - C_nr^n(1-\epsilon)^n}{C_nr^n} &= 1 - (1-\epsilon)^n\\ \frac{V_{rind}}{V_{total}} &= 1 - (1 - r)^d \end{align}

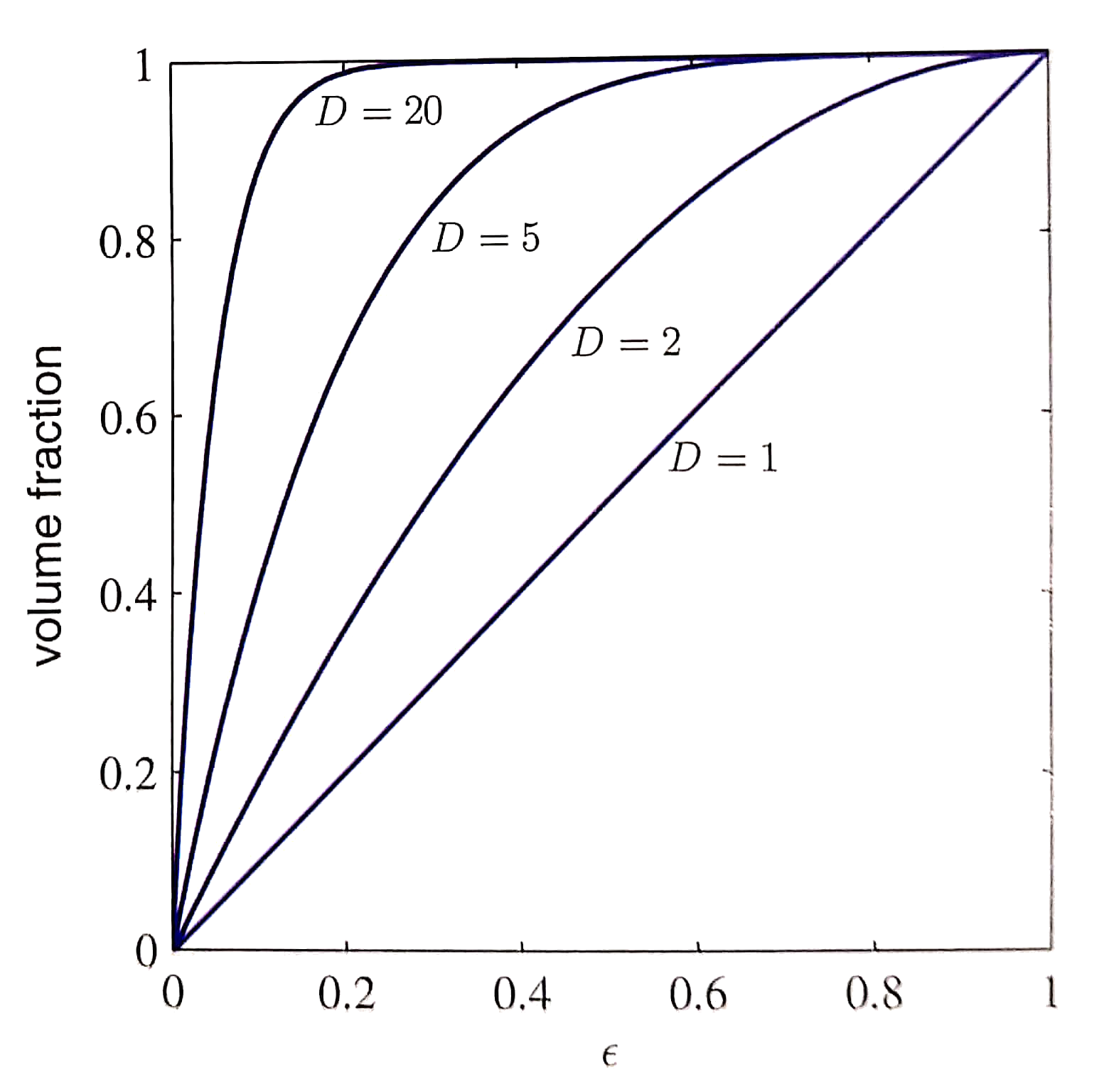
Fraction of volume

\[ \frac{V_{rind}}{V_{total}} = 1 - (1 - \epsilon)^D \]

What volume fraction of a hyper-melon does the rind occupy if it takes up an $\epsilon$ fraction of its radius?

$fraction$

Gaussian distribution

\[ G({\bf x}) = \frac{1}{(2\pi)^{K/2} |{\bf C}|^{1/2}} e^{-\frac{1}{2}{\bf x}^{\;{\rm T}} {\bf C}^{-1} {\bf x}} \]

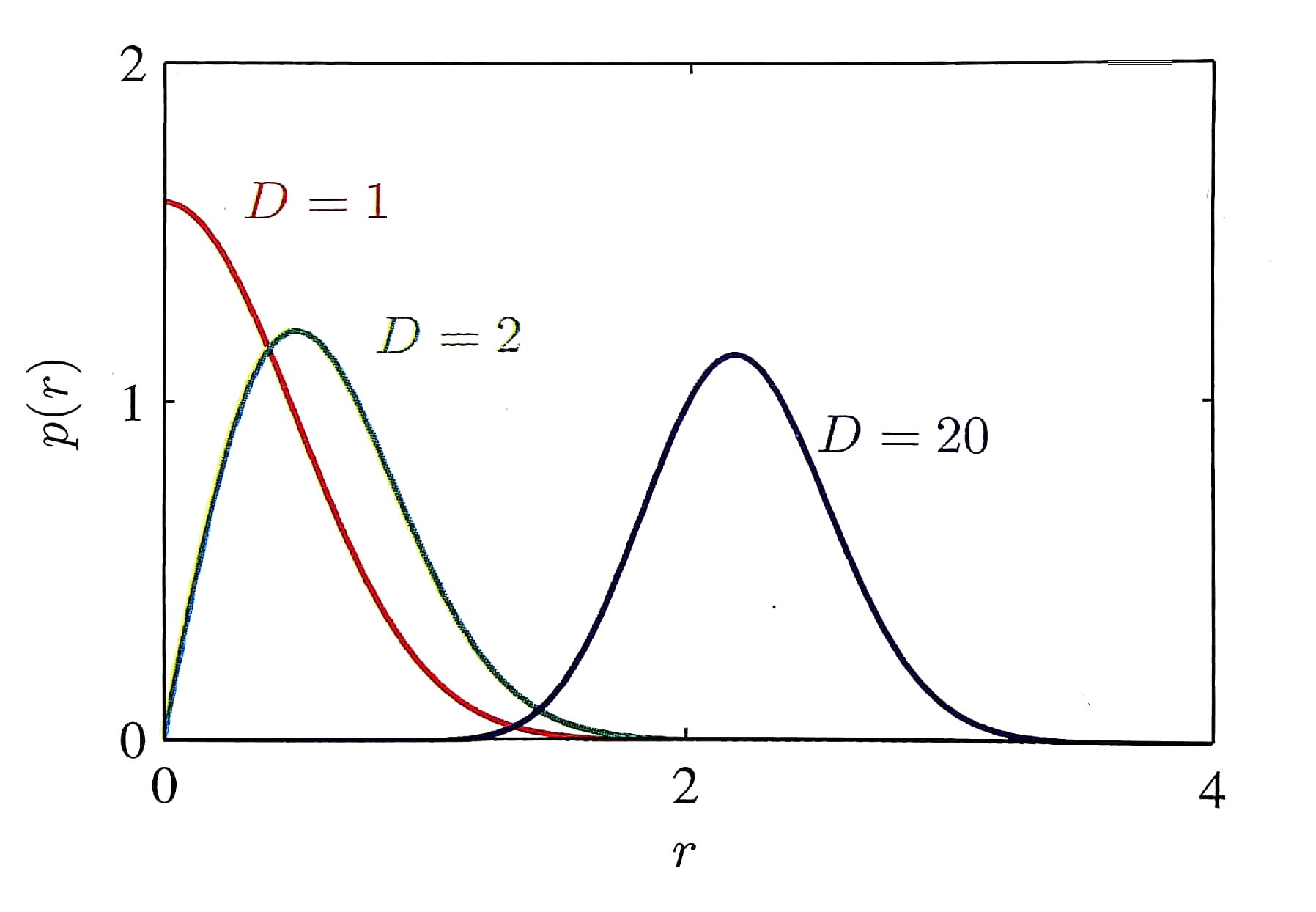
What's the probability of a random sample falling on a radius $r$ "shell" around the mean? density estimation

1. Gaussian density G(x) is maximized at the mean x = 0.
2. But what is the probability mass in a thin spherical shell of radius r and thickness dr?
3. Surface area of a sphere in D dimensions grows as r^(D-1).
4. The radial probability mass is p(r)dr ∝ r^(D-1) * exp(-r² / 2) dr.
5. For D = 1, this peaks at r = 0.
6. For general D, maximizing r^(D-1) * exp(-r²/2) yields peak radius r* = √(D - 1) ≈ √D.
7. The Gaussian Annulus Theorem: In high dimensions, random Gaussian vectors almost never fall near the center! Virtually all probability mass lives in a razor-thin spherical shell ("soap bubble") at radius √D.

What if the flesh isn't in the center?

Question: What is the probability of randomly hitting the flesh?

1. Suppose the sweet flesh (target) is a small sub-sphere of radius εR located anywhere inside the watermelon.
2. Volume of the target: V_target = C_d * (εR)^d.
3. Volume of the entire watermelon: V_total = C_d * R^d.
4. Probability of a uniform random sample landing in the target: P(hit) = V_target / V_total = ε^d.
5. If ε = 0.10 (target is 10% of radius):
- In 1D: P = 10%
- In 2D: P = 1%
- In 3D: P = 0.1%
- In 10D: P = 10^(-10) (one in ten billion)
- In 50D: P = 10^(-50) (astronomically impossible).
6. This directly leads to the next slide on multiple random restarts in optimization!

Local minima and multiple starts

blackboard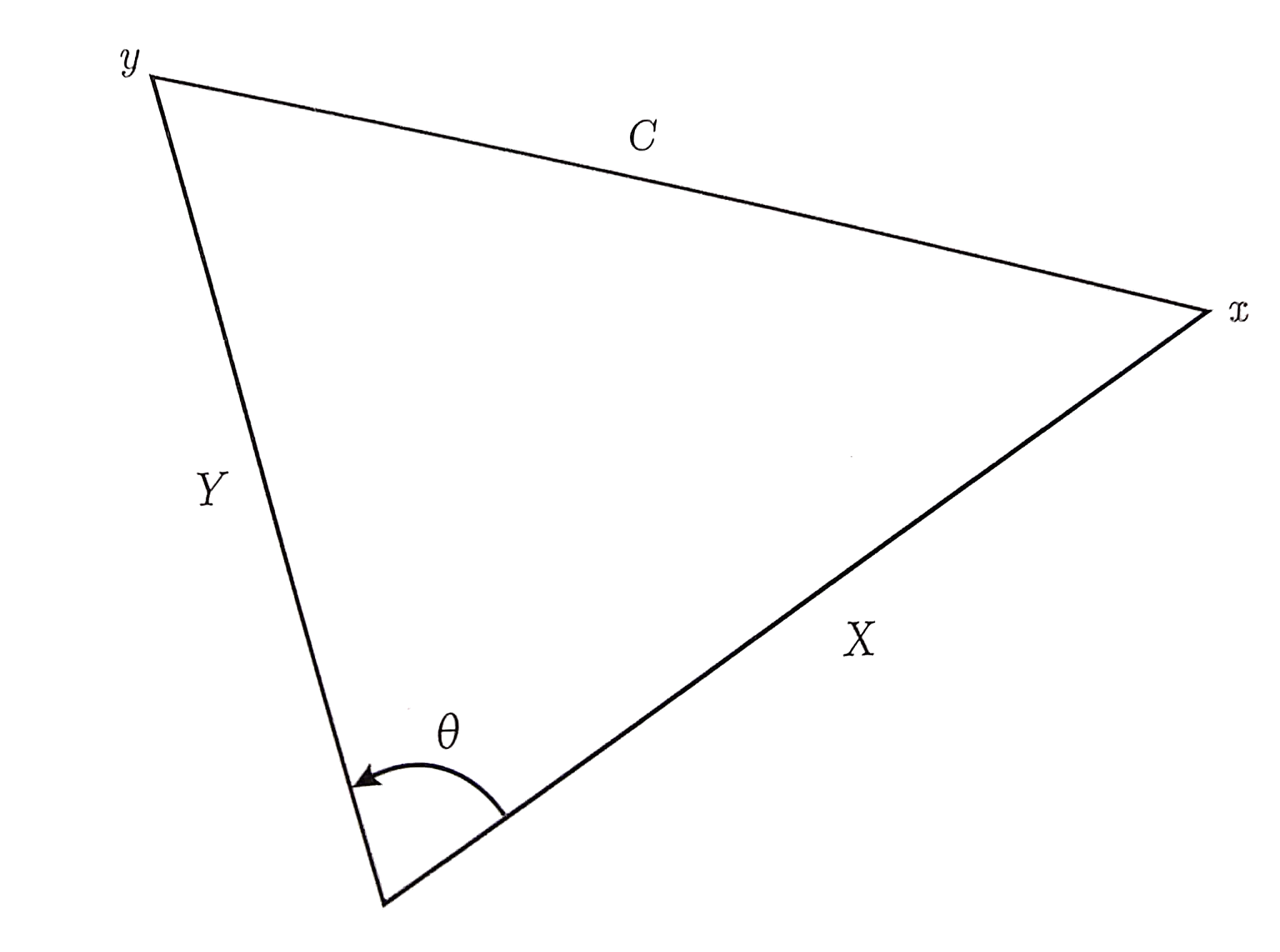

Blackboard walkthrough:
1. Draw a 1D non-convex loss function with multiple local minima and one global minimum.
2. In 1D/low dimensions, the standard recipe to find the global minimum is 'multiple random restarts' — sample initial points uniformly at random and run gradient descent.
3. Now analyze this in D dimensions: Suppose the basin of attraction around the global minimum has radius ε (fraction of domain width).
4. As shown in the previous slide, the volume of this basin is ε^D.
5. If ε = 0.1 and D = 100, the probability of a random restart landing in the global basin is 10^(-100). Even running trillions of restarts on a supercomputer for the lifetime of the universe will never hit it!
6. Conclusion: Random restart optimization completely breaks down in high dimensions.
7. Why deep learning works: Modern overparameterized neural networks don't rely on finding isolated narrow global minima. In high dimensions, local minima largely disappear or have similar loss, and optimization is dominated by saddle points, which first-order methods (SGD with momentum) can escape.

Law of cosines

Angles between vectors

$\cos\theta = \frac{1}{\sqrt{n}} \to 0$ and $\theta \to \frac{\pi}{2}$
$\cos\theta = \frac{\sum_{k=1}^n x_k y_k}{XY}$
Draw vectors to two random points $(\pm 1, \pm 1, \pm 1. \dots, \pm 1)$
$\cos\theta = \frac{\sum_{k=1}^n (\pm 1)}{n} \stackrel{a.s.}\to 0$, as $n \to \infty$

Angles between vectors

Dim: D = 2

Mean Angle: θ̄ = 90.0°

Std Dev: σ_θ ≈ 40.5°

Near-Orthogonal (90±10°): 11.1%

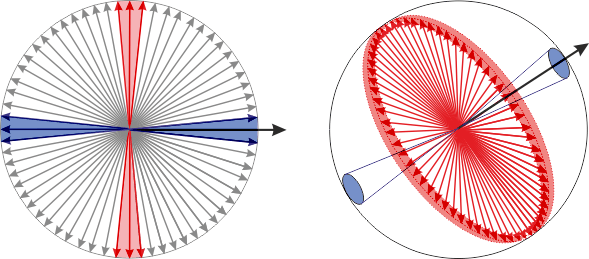
D = 2: Angles are uniformly spread across 0° to 180°.

Dim D: 2

3D:

1. 3D Hypersphere Projection Explorer: Demonstrates measure concentration on angles between random vectors.
2. Left panel (3D rotatable sphere projection):
- The red arrow represents a fixed reference vector u (North Pole).
- In D = 3, points are distributed uniformly across the entire 3D sphere surface S² (Archimedes' theorem). You can click, grab, and rotate the globe with your mouse in any direction to see the uniform spread!
- In high dimensions (D = 10, 50, 100), the points on S^(D-1) collapse into a flat, glowing equatorial belt orthogonal to u.
- Interactive controls: Use your mouse or the buttons (Angled, Top View, Side View) to rotate the 3D sphere. Looking down from the North Pole ('Top View'), the points form a ring around u; looking edge-on ('Side View'), the entire distribution flattens into a single razor-thin horizontal line perpendicular to u!
3. Right panel (angle density & histogram):
- Shows theoretical density p(θ) ∝ (sin θ)^(D-2) overlaid with a live empirical histogram of 600 random vector pairs.
- At D = 2, the density is completely flat: any angle from 0° to 180° is equally likely.
- As D increases, the standard deviation collapses as σ ≈ 1/√D (in radians). In D = 100, over 90% of random pairs lie strictly within ±10° of perpendicular (80°–100°).
4. Takeaway: In high dimensions, random vectors are almost certainly orthogonal. This is why embedding spaces can store thousands of independent concepts without interference.

Probability of orthogonality

Estimating probability

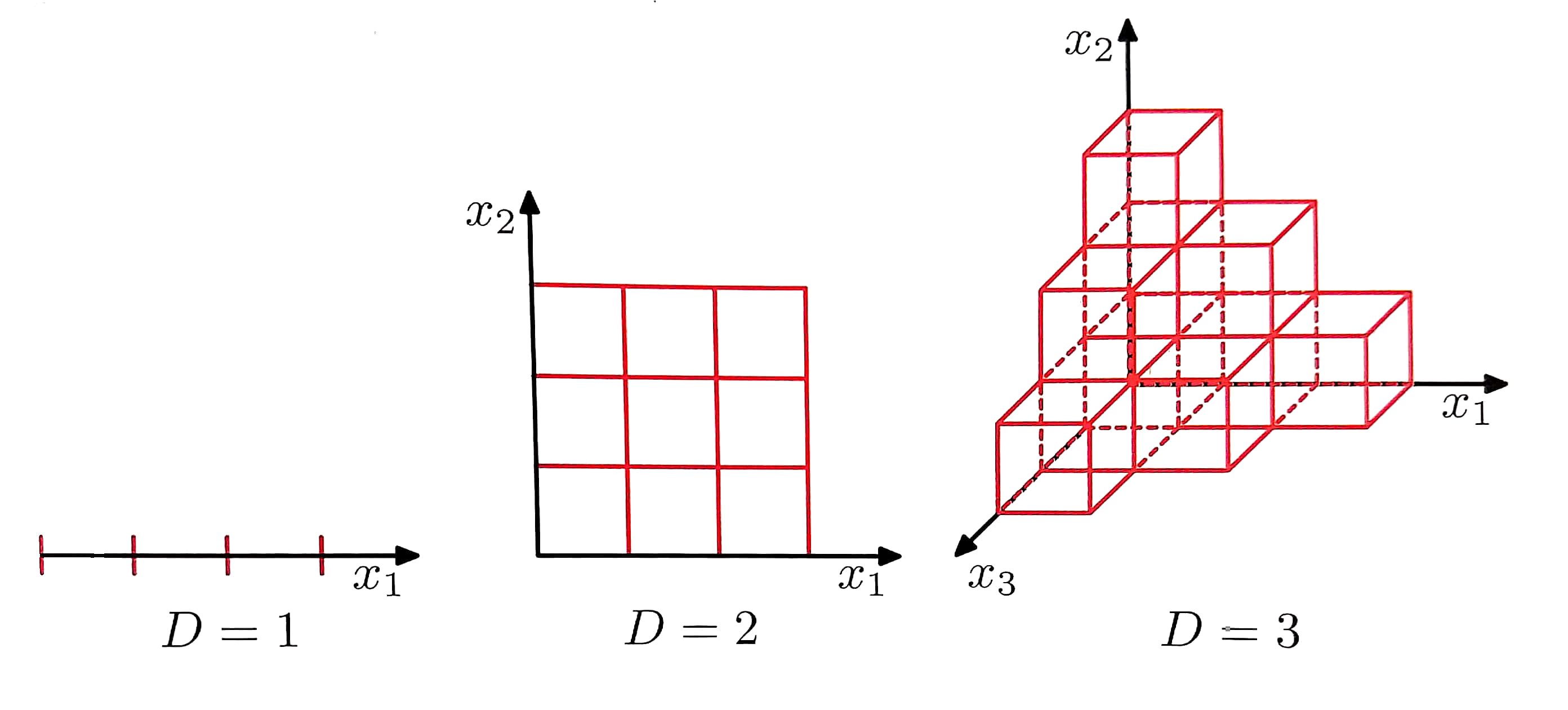
Question: What's the minimum number of samples we need to estimate a $d$ dimensional density in a cube?

4x4 paradox

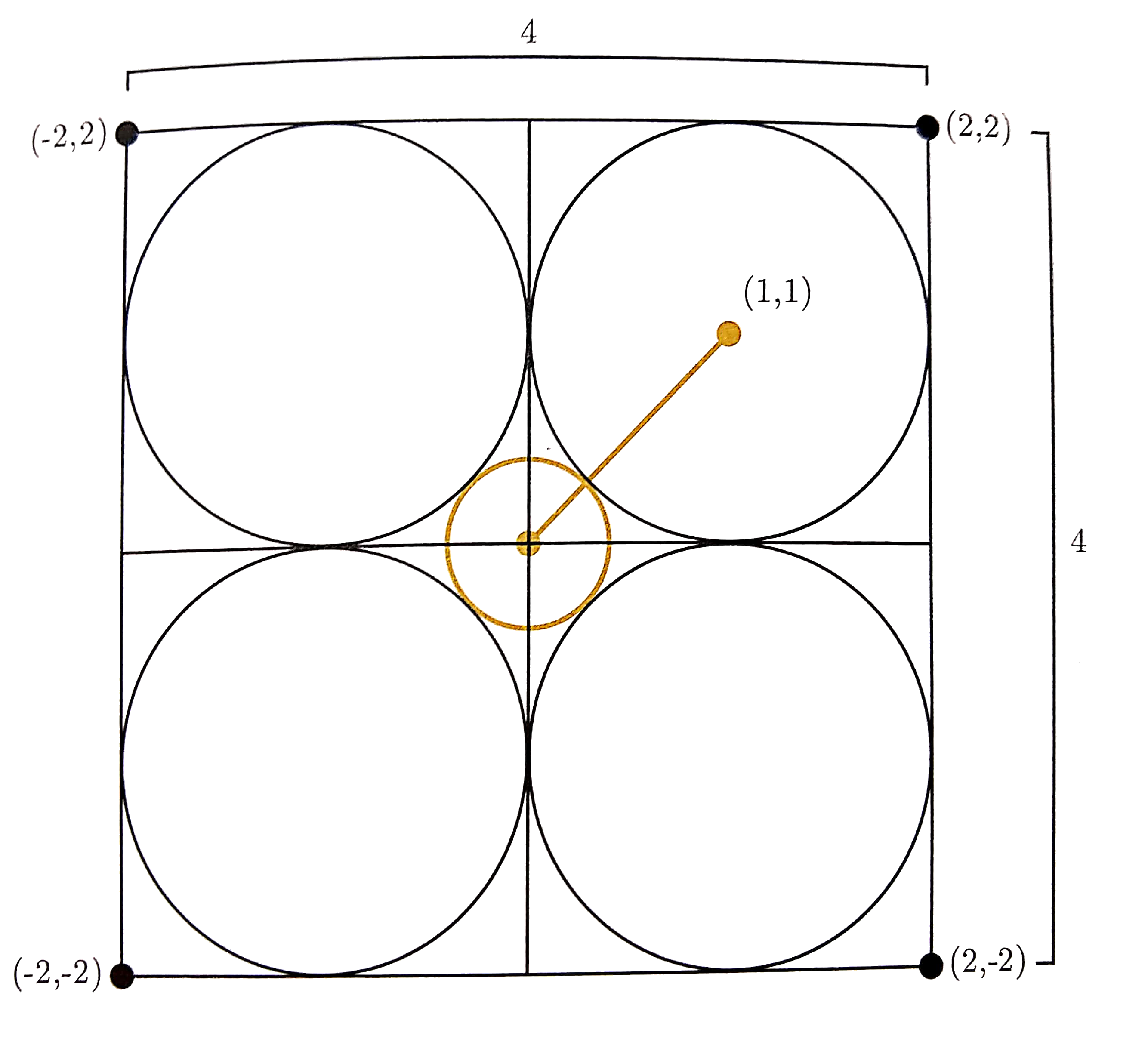
Hamming's 4x4 box sphere packing paradox:
1. In 2D, consider a box of side 4 centered at the origin: [-2, 2]^2.
2. In each corner, place a sphere of radius 1 centered at (±1, ±1).
3. In the center (0, 0), place an inner sphere tangent to the corner spheres.
4. Distance from origin to corner center is √(1² + 1²) = √2 in 2D, and √(1² + ... + 1²) = √d in d dimensions.
5. Since corner spheres have radius 1, the inner sphere radius is r = √d - 1.
6. Key milestones:
- d = 2: r = √2 - 1 ≈ 0.414 (small inner sphere)
- d = 4: r = √4 - 1 = 1.0 (inner sphere is EQUAL in size to corner spheres)
- d = 9: r = √9 - 1 = 2.0 (inner sphere touches the flat faces of the 4×4 box)
- d ≥ 10: r = √10 - 1 ≈ 2.162 > 2.0 (inner sphere EXTENDS OUTSIDE the box!).
7. Resolving the paradox & why spheres shrink:
- In high dimensions, the corner spheres' volume shrinks to zero relative to the cube: V_spheres / V_cube = (π/4)^(d/2) / Γ(d/2+1) → 0.
- The corners of the hypercube pull far away from the center (diagonal length 2√d). The corner spheres become tiny specks deep in the far-flung corners, leaving vast empty channels along the coordinate axes where the central sphere expands outside the faces!

Alternative distances

L₂ (Euclidean Norm)

‖x‖₂ = √(x₁² + x₂²) = 1

Probe: x = (0.80, 0.60)

‖x‖₁ = 1.40 | ‖x‖₂ = 1.00

‖x‖_p = 1.00 | ‖x‖_∞ = 0.80

Click/drag canvas to move probe x

Norm p: 2.0

1. Definition of Lp (Minkowski) distance: D_p(x, y) = (Σ |x_i - y_i|^p)^(1/p).
2. Geometry of unit balls:
- p = 1 (Manhattan / L1): Diamond shape with sharp vertices on the coordinate axes. When level sets of linear loss touch this diamond, they hit the corners, producing exact zero coefficients — this is why L1 regularization (Lasso) induces sparsity!
- p = 2 (Euclidean / L2): Standard rotational invariant circle.
- p = ∞ (Chebyshev / L∞): Square shape with sides parallel to coordinate axes: D_∞(x, y) = max_i |x_i - y_i|.
- p < 1: Non-convex star shapes (quasi-norms; triangle inequality fails, but induces extreme sparsity).
3. Curse of Dimensionality on Distance Metrics (Aggarwal et al. 2001):
- In high dimensions, under L2, (d_max - d_min) / d_min → 0. The distance from any query point to its nearest neighbor approaches the distance to its farthest neighbor! All data points become equidistant.
- Aggarwal proved that lower p norms (and even fractional norms p < 1) degrade more slowly than L2, retaining meaningful contrast longer in high dimensions.

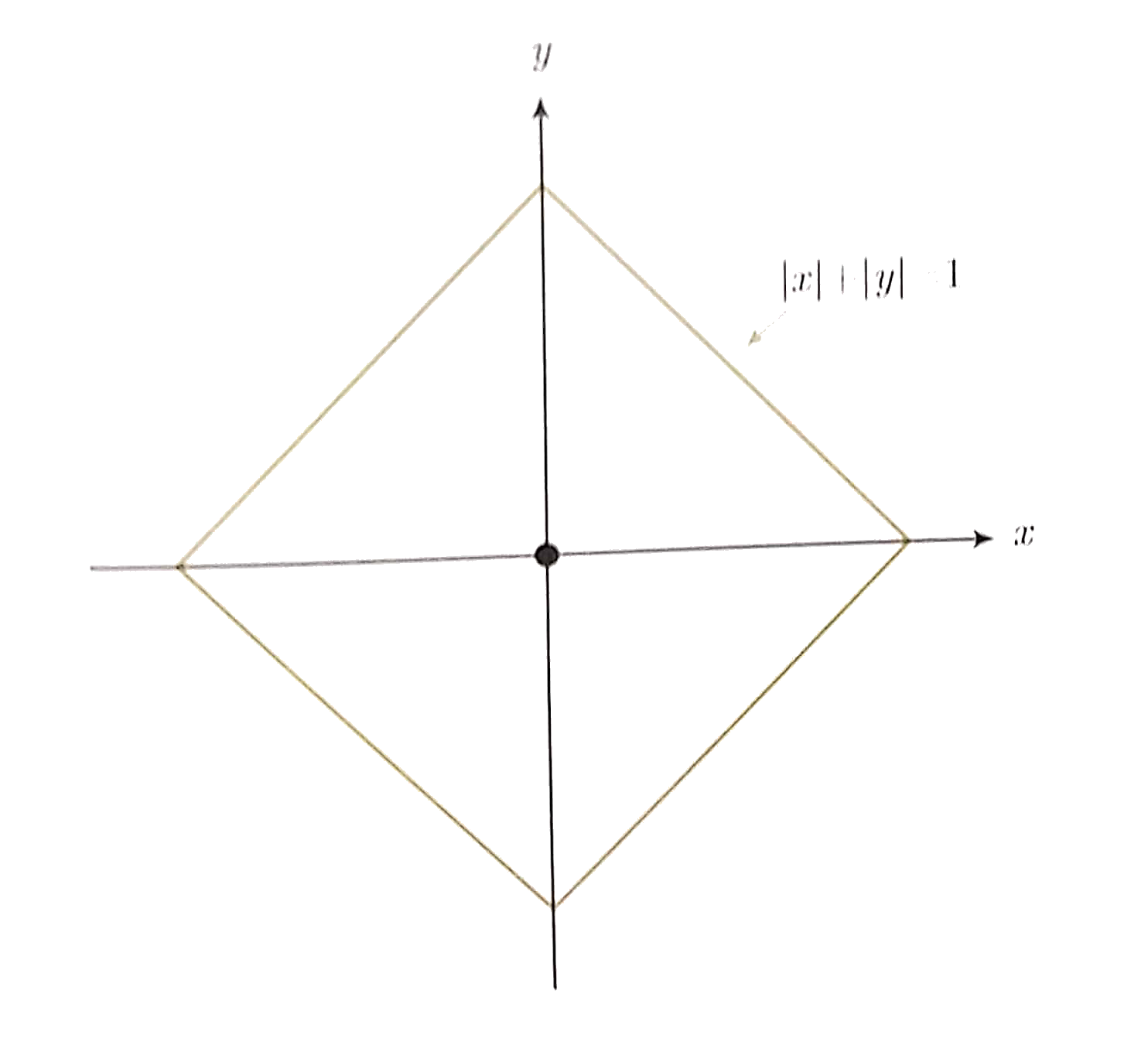
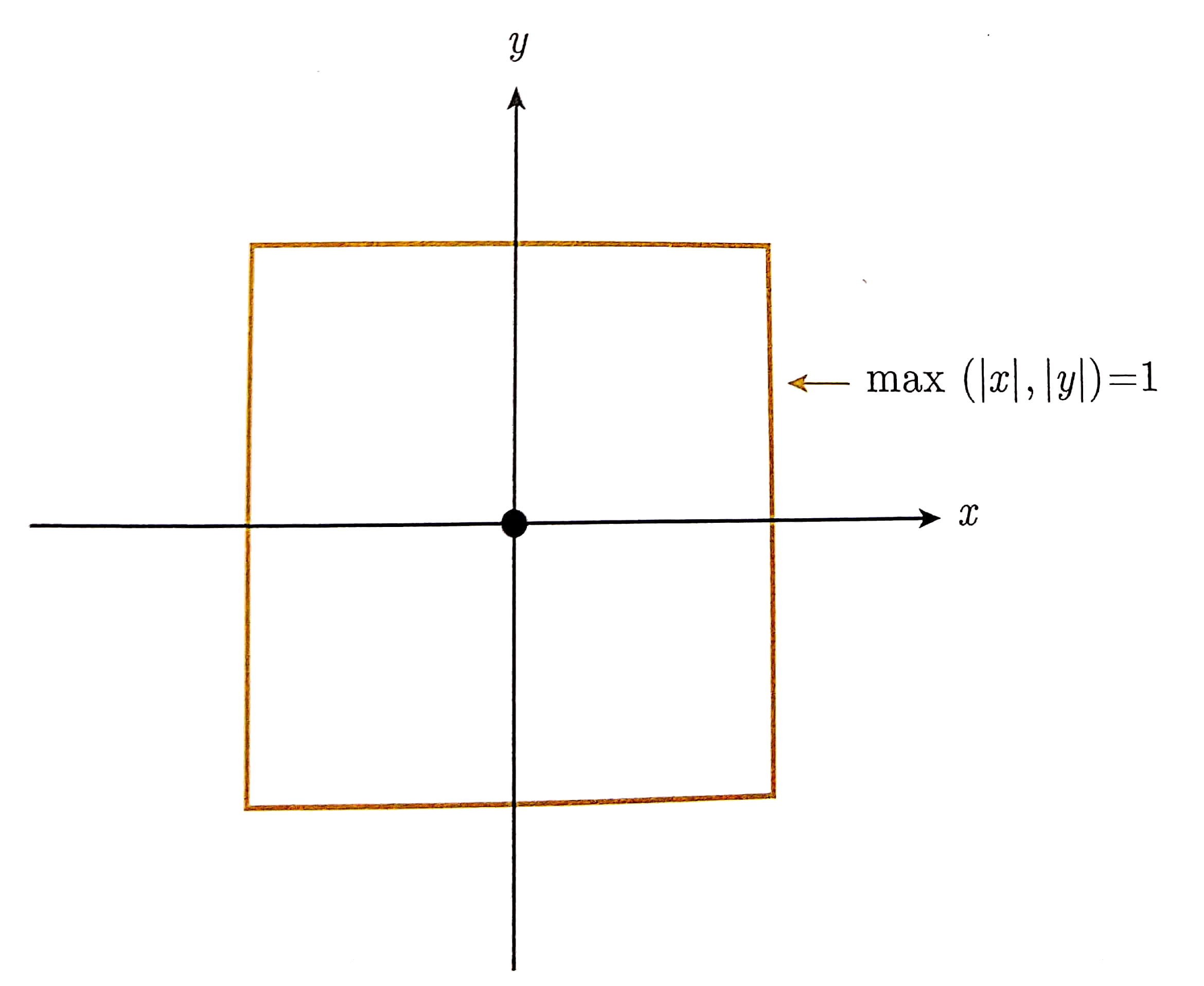
Conditions on a metric

$D(x,y) \ge 0$ (non-negative)
$D(x,y) = 0$ iff $x=y$ (identity)
$D(x,y) = D(y,x)$ (symmetry)
$D(x,y) + D(y,z) \ge D(x,z)$ (triangle inequality)

Case study: an average human

1. Context: In the late 1940s, the US Air Force was baffled by alarming crash rates during routine flights. Pilots were losing control of planes with no mechanical failure.
2. Background: Cockpits had been designed around the 'average pilot' measured back in 1926.
3. Gilbert Daniels' 1950 Study: Lt. Gilbert S. Daniels measured 4,063 pilots across 10 physical dimensions (height, chest circumference, sleeve length, crotch height, torso height, etc.).
4. The Hypothesis: Daniels tested how many pilots fell within the middle 30% of the distribution (a very generous definition of 'average') on all 10 dimensions.
5. Question to class: Out of 4,063 pilots, how many were average on all 10 traits?
6. The Result: Exactly ZERO (0 out of 4,063)! Not a single pilot was average across 10 dimensions. Even across just 3 dimensions, less than 3.5% were average.
7. The Math: (0.30)^10 ≈ 0.000006 (0.0006%).
8. The Engineering Fix: The Air Force realized a cockpit designed for the average fits nobody. They mandated adjustable seats, adjustable rudder pedals, and adaptable harnesses — birth of ergonomic design.
9. Takeaway for Machine Learning: In high-dimensional data, there is no such thing as an 'average' point. Every single data point is an extreme outlier in some combination of features!

Take-home message

"Abandon common sense, all ye who enter $\mathbb{R}^D$ ($D \gg 3$)."

🍉 Melons: All rind, no flesh — everything is on the surface ($1 - (1-\epsilon)^D \to 1$)
🦔 Hypercubes: All thorns, no body — volume lives in the diagonal corners
📐 Random vectors: Almost surely perpendicular ($\theta \stackrel{a.s.}\to 90^\circ$)
📏 Distances: Everything is equidistant ($(d_{\max} - d_{\min})/d_{\min} \to 0$)
👤 Average human: A pure myth — everyone is an extreme outlier

Our 3D intuition is a local illusion. In high dimensions, you must trust the math.

Wrap-up talking points for Lecture 07:
1. Why it's called a 'curse': Human brains evolved to throw rocks and hunt mammoths in 3 dimensions. Our spatial common sense completely fails in high dimensions.
2. Review the 5 counter-intuitive pillars we covered today:
- Surface concentration: In 100D, a 2% rind takes 87% of the melon. Any probability mass is pushed onto a thin spherical skin (Gaussian Annulus Theorem).
- Corner concentration: The Hamming 4x4 inner sphere punches outside because high-D cubes are shaped like spiky sea urchins.
- Orthogonality: Any two random vectors are orthogonal. You can embed exponentially many nearly orthogonal vectors in a feature space.
- Distance concentration: Nearest neighbor search degrades because all pairwise distances become identical under L2.
- The average pilot fallacy: A cockpit or model designed for the 'average' user fits exactly 0% of your data.
3. Takeaway for Machine Learning: When you train models with hundreds or thousands of features (embeddings, vision, LLMs), remember you are navigating an overwhelmingly empty, spike-dominated, hyper-orthogonal geometry. Always verify your assumptions with linear algebra rather than 3D intuition!

Reading list

p. 33 of "Pattern recognition and Machine Learning" by C. Bishop
p. 22 of "The Elements of Statistical Learning" by T. Hastie, R. Tibshirani, and J. Friedman
Chapter 9 of "The Art of Doing Science and Engineering: Learning to Learn" by R. Hamming