Advanced Machine Learning

06: regression and PCA

Schedule (you are here )

#	date	topic	description
1	24-Aug-2026	Introduction
2	26-Aug-2026	Foundations of learning	Drop/Add
3	31-Aug-2026	PAC learnability	HW1
4	02-Sep-2026	Linear learning models
5	07-Sep-2026	Labor Day Holiday	Holiday
6	09-Sep-2026	Principal Component Analysis	Project ideas
7	14-Sep-2026	Curse of Dimensionality	HW2, HW1 due
8	16-Sep-2026	Bayesian Decision Theory
9	21-Sep-2026	Parameter estimation: MLE
10	23-Sep-2026	Parameter estimation: MAP & NB	finalize teams
11	28-Sep-2026	Logistic Regression	HW3, HW2 due
12	30-Sep-2026	Kernel Density Estimation
13	05-Oct-2026	Support Vector Machines
14	07-Oct-2026	Matrix Factorization
15	12-Oct-2026	* Midterm	Exam, HW3 due
16	14-Oct-2026	k-means clustering
17	19-Oct-2026	Invited: Intro to Causal Learning I

#	date	topic	description
18	21-Oct-2026	Invited: Intro to Causal Learning II
19	26-Oct-2026	* Mid-point projects checkpoint	HW4, P
20	28-Oct-2026	Expectation Maximization
21	02-Nov-2026	Stochastic Gradient Descent
22	04-Nov-2026	Automatic Differentiation
23	09-Nov-2026	Nonlinear embedding approaches	HW5, HW4 due
24	11-Nov-2026	Model comparison
25	16-Nov-2026	Model Calibration
26	18-Nov-2026	Convolutional Neural Networks
27	23-Nov-2026	Thanksgiving Break	Holiday
28	25-Nov-2026	Thanksgiving Break	Holiday
29	30-Nov-2026	Word Embedding
30	02-Dec-2026	Project Final Presentations	HW5 due, P
31	07-Dec-2026	Presentation spillover / Exam prep	Classes End
32	09-Dec-2026	* Final Exam	Exam
33	16-Dec-2026	Project Reports	due
34	17-Dec-2026	Grades due 5 p.m.	PAWS

Outline for the lecture

Linear Regression
Linear Algebra Refresher
Spectral Theorem
Principal Component Analysis
Dimensionality Reduction Demo
Take Home Points

Francis Galton

Carl Friedrich Gauss

Linear regression

Adrien-Marie Legendre

Least Mean Squares

Linear Regression

$f(\vec{w}) = \frac{1}{n} \sum_{i}^{n} (\vec{w}^T\vec{x}_i - y_i)^2$

Let us write in matrix form:
$f(\vec{w}) =\frac{1}{n}(\bf{X}\vec{w} - \vec{y})^T(\bf{X}\vec{w} - \vec{y})$

Expanding:
$f(\vec{w}) =\frac{1}{n}(\vec{w}^T\bf{X}^T\bf{X}\vec{w} - 2\vec{w}^T\bf{X}^T\vec{y} + \vec{y}^T\vec{y})$

Dropping $\vec{y}$:
$f(\vec{w}) =\frac{1}{n}(\vec{w}^T\bf{X}^T\bf{X}\vec{w} - 2\vec{w}^T\bf{X}^T\vec{y})$

Using:
$\frac{\partial \vec{x}^T\bf{B}\vec{x}}{\partial \vec{x}} = (\bf{B} + \bf{B}^T)\vec{x}$
$\frac{\partial f(\vec{w})}{\partial \vec{w}} =\frac{2}{n}(\bf{X}^T\bf{X}\vec{w} - \bf{X}^T\vec{y})$

Minimizing LMS

$\frac{\partial f(\vec{w})}{\partial \vec{w}} =\frac{2}{n}(\bf{X}^T\bf{X}\vec{w} - \bf{X}^T\vec{y})$

$\frac{\partial f(\vec{w})}{\partial \vec{w}} = 0 $

$\bf{X}^T\bf{X}\vec{w} - \bf{X}^T\vec{y} = 0$
$\bf{X}^T\bf{X}\vec{w} = \bf{X}^T\vec{y}$
$\vec{w} = (\bf{X}^T\bf{X})^{-1}\bf{X}^T\vec{y}$

$\bf{X}^{\dagger} = (\bf{X}^T\bf{X})^{-1}\bf{X}^T$ - pseudoinverse

$\bf{X}^{\dagger} = \lim_{\epsilon \to 0}(\bf{X}^T\bf{X} + \epsilon\bf{I})^{-1}\bf{X}^T$ - always exists

Least Mean Squares regression

Least Mean Squares single sample

Fitting data: which is correct?

Everyone believes in the Gaussian law of errors. The experimentalists think it is a mathematical theorem, and the mathematicians think it is an established experimental fact.
-Henri Poincaré

Different ways to fit a line

Fitting Lines: OLS vs PCA / Orthogonal Distance

OLS (Y on X): y = 0.00x + 0.0 | RSS_Y = 0.0

OLS (X on Y): x = 0.00y + 0.0 | RSS_X = 0.0

PCA Line: θ = 0.0° | RSS_⊥ = 0.0

PCA Variance Explained: 0.0%

● Drag purple outlier | Click to add points

Mode:

Rotate: 35°

σ_Y: σ_X:

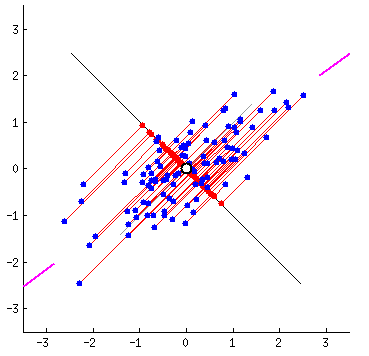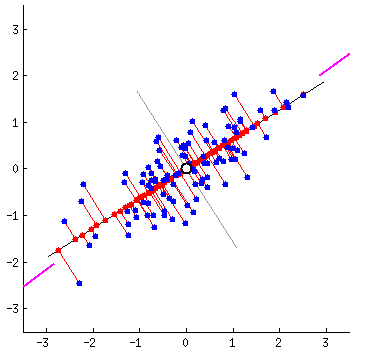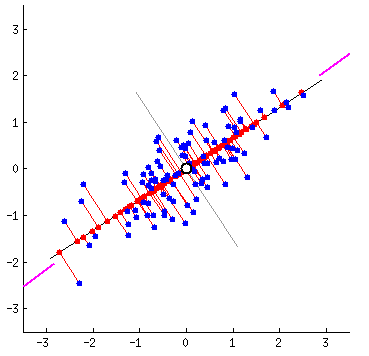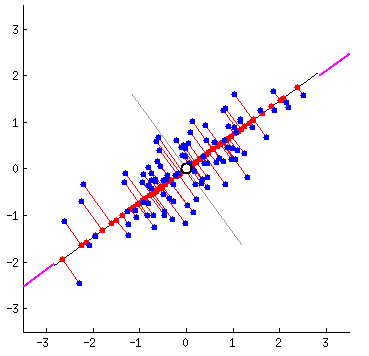
Linear Algebra Refresher

Inner product

Let ${\bf x} = \left[\begin{array}{ccc}1 & 2 & 3\end{array}\right]^{\rm T}$. The inner product of ${\bf x}$ with itself, or ${\bf x}^{T}{\bf x}$ is a scalar: $$ \left[ \begin{array}{ccc} 1 & 2 & 3 \end{array} \right] \left[ \begin{array}{c} 1\\ 2\\ 3 \end{array} \right] = 1 \cdot 1 + 2 \cdot 2 + 3 \cdot 3 = 14. $$

Outer product

The outer product of $\bf{x}$ with itself, or ${\bf x}{\bf x}^{\;{\rm T}}$ is a matrix: \[ \left[ \begin{array}{c} 1\\ 2\\ 3 \end{array} \right] \left[ \begin{array}{ccc} 1 & 2 & 3 \end{array} \right] = \left[ \begin{array}{ccc} 1 & 2 & 3\\ 2 & 4 & 6\\ 3 & 6 & 9 \end{array} \right] \]
which was obtained as
\[ \left[ \begin{array}{c} 1\\ 2\\ 3 \end{array} \right] \left[ \begin{array}{ccc} 1 & 2 & 3 \end{array} \right] = \left[ \begin{array}{c|c|c} 1\left[ \begin{array}{c} 1\\ 2\\ 3 \end{array} \right]& 2\left[ \begin{array}{c} 1\\ 2\\ 3 \end{array} \right]& 3\left[ \begin{array}{c} 1\\ 2\\ 3 \end{array} \right] \end{array} \right]. \]

Spectral Theorem

Change of basis

Consider a linear transform, ${\bf P}_{\cal B}$, and its inverse, ${\bf P}^{-1}_{\cal B}$, which map a vector back and forth between its representation in the standard basis and its representation in the basis, ${\cal B}$

$$ \begin{array}{ccc} & {\bf P}_{\cal B} & \\ \vec{u} & \stackrel{\longrightarrow}{\longleftarrow} & \left[\vec{u}\right]_{\cal B}\\ & {\bf P}^{-1}_{\cal B} & \end{array} $$

Which basis?

Let ${\cal B}$ consist of $N$ basis vectors, $\vec{b}_1 \dots \vec{b}_N$. Since $\left[{\bf u}\right]_{\cal B}$ is the representation of $\vec{u}$ in ${\cal B}$, it follows that

\[ \vec{u} = \left(\left[\vec{u}\right]_{\cal B}\right)_1 \vec{b}_1 + \left(\left[\vec{u}\right]_{\cal B}\right)_2 \vec{b}_2 + \dots \left(\left[\vec{u}\right]_{\cal B}\right)_N \vec{b}_N. \]

But that's a projection

\[ \vec{u} = \left(\left[\vec{u}\right]_{\cal B}\right)_1 \vec{b}_1 + \left(\left[\vec{u}\right]_{\cal B}\right)_2 \vec{b}_2 + \dots \left(\left[\vec{u}\right]_{\cal B}\right)_N \vec{b}_N \]

But this is just the matrix vector product $\vec{u} = {\bf B}\left[\vec{u}\right]_{\cal B}$

\[ {\bf B} = \left[\begin{array}{c|c|c|c}{\bf b}_1 & {\bf b}_2 & \dots & {\bf b}_N\end{array}\right] \]

$$ \begin{array}{ccc} & {\bf P}_{\cal B} & \\ \vec{u} & \stackrel{\longrightarrow}{\longleftarrow} & \left[\vec{u}\right]_{\cal B}\\ & {\bf P}^{-1}_{\cal B} & \end{array} $$

We see that

\[ \begin{array}{lcl } {\bf P}_{\cal B} &=& {\bf B}^{-1}\\ {\bf P}^{-1}_{\cal B} &=& {\bf B} \end{array} \]

Similarity Transforms

Consider a linear transformation represented in the standard basis by the matrix ${\bf A}$. We seek $\left[{\bf A}\right]_{\cal B}$, i.e., the representation of the corresponding linear transformation in the basis ${\cal B}$

\[ \begin{array}{ccc} \vec{u} & \stackrel{{\bf A}}{\longrightarrow} & {\bf A}\vec{u}\\ \uparrow {\bf B} & & \downarrow {\bf B}^{-1}\\ \left[\vec{u}\right]_{\cal B} & \stackrel{\left[{\bf A}\right]_{\cal B}\;\;\;}{\longrightarrow} & \left[{\bf A}\vec{u}\right]_{\cal B} \end{array} \]

Similarity Transforms

\[ \left[{\bf A}\right]_{\cal B} = {\bf B}^{-1}{\bf A}{\bf B}. \] ${\bf A}$ and $\left[{\bf A}\right]_{\cal B}$ are related by a similarity transform.

Basis of eigenvectors

Let ${\bf A}$ be a representation of a transform in the standard basis and let the columns of ${\bf X}$ be the eigenvectors of ${\bf A}$ (symmetric). Then ${\bf X}$ and ${\bf X}^{\rm T}={\bf X}^{-1}$ take us back and forth between the standard basis and ${\cal X}$:

\[ \begin{array}{ccc} & {\bf X}^{\rm T} & \\ {\bf u} & \stackrel{\longrightarrow}{\longleftarrow} & \left[{\bf u}\right]_{\cal X}\\ & {\bf X} & \end{array} \]

Diagonalization of Symmetric Matrices

The matrix we seek maps $\left[{\bf u}\right]_{\cal X}$ into $\left[{\bf A}{\bf u}\right]_{\cal X}$:

\[ \begin{array}{ccc} {\bf u} & \stackrel{{\bf A}}{\longrightarrow} & {\bf A}{\bf u}\\ \uparrow {\bf X} & & \downarrow {\bf X}^{\rm T}\\ \left[{\bf u}\right]_{\cal X} & \stackrel{\left[{\bf A}\right]_{\cal X}\;\;\;}{\longrightarrow} & \left[{\bf A}{\bf u}\right]_{\cal X} \end{array} \]

which is (from the diagram): \[ \Lambda = {\bf X}^{\rm T}{\bf A}{\bf X}. \] Note, $\Lambda$ is diagonal with $\Lambda_{ii}=\lambda_i$

Spectral Theorem for Symmetric Matrices

Any symmetric $N \times N$ matrix, ${\bf A}$, with $N$ distinct eigenvalues, can be factored as follows: \[ {\bf A} = {\bf X} \Lambda {\bf X}^{\rm T} \] where $\Lambda$ is $N \times N$ and diagonal, ${\bf X}$ and ${\bf X}^{\rm T}$ are $N \times N$ matrices, and the $i$-th column of ${\bf X}$ (equal to the $i$-th row of ${\bf X}^{\rm T}$) is an eigenvector of ${\bf A}$: \[ \lambda_i {\bf x}_i = {\bf A}{\bf x}_i \] with eigenvalue $\Lambda_{ii} = \lambda_i$.

Spectral Theorem (note)

Note that ${\bf x}_i$ is orthogonal to ${\bf x}_j$ when $i \neq j$: \[ \left({\bf X}{\bf X}^{\rm T}\right)_{ij} = \delta_{ij} = \left\{\begin{array}{ll}1 & {\rm if}\;\;i=j\\ 0 & {\rm otherwise.}\end{array} \right. \] In other words, ${\bf X}{\bf X}^{\rm T} = {\bf I}$. Consequently, \[ {\bf X}^{\rm T} = {\bf X}^{-1} \]

Spectral Theorem (cont.)

Let's rewrite ${\bf A} = {\bf X} \Lambda {\bf X}^{\rm T}$ using the definition of matrix product and the fact that $\Lambda$ is diagonal:

\begin{eqnarray*} \left({\bf A}\right)_{ij} & = & \sum_{k=1}^N \left({\bf X}\right)_{ik} \Lambda_{kk} \left({\bf X}^{\rm T}\right)_{kj} \end{eqnarray*}

Spectral Theorem (cont.)

Since ${\bf X} = \left[\begin{array}{c|c|c|c} {\bf x}_1 & {\bf x}_2 & \cdots & {\bf x}_N\end{array}\right]$ and $\Lambda_{kk} = \lambda_k$

\begin{eqnarray*} \left({\bf A}\right)_{ij} & = & \sum_{k=1}^N \left({\bf X}\right)_{ik} \Lambda_{kk} \left({\bf X}^{\rm T}\right)_{kj} \end{eqnarray*}

\begin{eqnarray*} \left({\bf A}\right)_{ij} & = & \sum_{k=1}^N \left({\bf x}_k\right)_i \lambda_k \left({\bf x}_k\right)_j = \sum_{k=1}^N \left(\lambda_k {\bf x}_k {\bf x}_k^{\rm T}\right)_{ij} \end{eqnarray*}

\begin{eqnarray*} {\bf A} & = & \sum_{k=1}^N \lambda_k {\bf x}_k {\bf x}_k^{\rm T},\text{ where } \lambda_k {\bf x}_k = {\bf A}{\bf x}_k \end{eqnarray*}

Spectral Theorem (cont.)

The spectral factorization of ${\bf A}$ is: \[ {\bf A} = \lambda_1 \vec{x}_1 \vec{x}^{\rm T}_1 + \lambda_2 \vec{x}_2 \vec{x}^{\rm T}_2 + \dots + \lambda_N \vec{x}_N \vec{x}^{\rm T}_N. \]

Note, each $\lambda_n {\bf x}_n {\bf x}^{\rm T}_n$ is a rank one matrix

Let ${\bf A}_i = \lambda_i \vec{x}_i \vec{x}^{\rm T}_i$. Now, because $\vec{x}^{\rm T}_i \vec{x}_i = 1$: \begin{eqnarray*} \lambda_i \vec{x}_i & = & \left(\lambda_i \vec{x}_i \vec{x}^{\rm T}_i \right)\vec{x}_i\\ & = & {\bf A}_i \vec{x}_i \end{eqnarray*} i.e., $\vec{x}_i$ is the only eigenvector of ${\bf A}_i$ and its only eigenvalue is $\lambda_i$.

Principal Component Analysis

Quadratic forms

Let $f({\bf x}) = {\bf x}^{\;{\rm T}}{\bf A}{\bf x}$ where ${\bf A}={\bf A}^{\rm T}$. In two-dimensions, we have \[ {\bf A} = \left[\begin{array}{cc} a & b\\ b & c \end{array}\right]\;\;\;{\rm and}\;\;\; {\bf x} = \left[\begin{array}{cc}x & y\end{array}\right]^{\rm T} \]

\[ {\bf A}{\bf x} = \left[\begin{array}{cc} a & b\\ b & c \end{array}\right] \left[\begin{array}{c} x\\ y \end{array}\right] = \left[\begin{array}{c} a x + b y\\ b x + c y \end{array}\right] \]

\[ {\bf x}^{\;{\rm T}}{\bf A}{\bf x} = \left[\begin{array}{cc} x & y \end{array}\right] \left[\begin{array}{c} a x + b y\\ b x + c y \end{array}\right] = a x^2 + 2 b x y + c y^2. \]

Quadratic forms

When ${\bf A}$ is positive definite, then \[ f({\bf x}) = {\bf x}^{\;{\rm T}}{\bf A}{\bf x} \] is a paraboloid and the level curves, \[ {\bf x}^{\;{\rm T}}{\bf A}{\bf x} = k \] are ellipses. A matrix is positive definite iff all of its eigenvalues are positive.

example

Let ${\bf A}=\left[\begin{array}{cc}5 & -2\\ -2 & 5\end{array}\right]$. Then ${\bf x}^{\;{\rm T}}A{\bf x}$ equals \[ 5 x^2 - 4xy + 5y^2 \]

Multivariate Gaussian Density

\[ G({\bf x}) = \frac{1}{(2\pi)^{K/2} |{\bf C}|^{1/2}} e^{-\frac{1}{2}{\bf x}^{\;{\rm T}} {\bf C}^{-1} {\bf x}} \]

$K$ is the number of dimensions and ${\bf C}$ is the $K \times K$ covariance matrix.

In the bivariate case

\[ {\bf C} = \left[ \begin{array}{cc} \sigma_{xx} & \sigma_{xy}\\ \sigma_{xy} & \sigma_{yy} \end{array} \right] \]

Note: If ${\bf C}$ is symmetric and positive definite, then ${\bf C}^{-1}$ is also symmetric and positive definite.

Covariance Matrix

An $N \times K$ matrix, $X$, where the $n$-th row is the $n$-th sample of a Gaussian distributed vector random variable, ${\bf x} = \left[x, y\right]^T$

For example, when $K=2$: \[ {\bf X} = \left[ \begin{array}{cc} x_1 & y_1\\ x_2 & y_2\\ \vdots & \vdots\\ x_N & y_N \end{array} \right] \]

Covariance Matrix

The sample mean of the $N$ samples is \[ {\bf \mu} = \frac{1}{N}\sum_{n=1}^N {\bf x}_n. \] We will assume that ${\bf \mu} = \left[0, 0 \right]^{T}$. If this is false, we can always make it true by subtracting ${\bf \mu}$ from each of the samples prior to constructing ${\bf X}$.

Covariance Matrix

Observe that

\begin{eqnarray*} {\bf X}^{\rm T} {\bf X} & = & \sum_{n=1}^N {\bf x}_n {\bf x}_n^{\;{\rm T}} = \left[ \begin{array}{cc} x_1 x_1 & x_1 y_1\\ x_1 y_1 & y_1 y_1 \end{array} \right] + \cdots + \left[ \begin{array}{cc} x_N x_N & x_N y_N\\ x_N y_N & y_N y_N \end{array} \right] \end{eqnarray*}

Consequently $$ \frac{1}{N}{\bf X}^{\rm T} {\bf X} = \left[ \begin{array}{cc} \langle xx\rangle & \langle xy\rangle\\ \langle xy\rangle & \langle yy\rangle \end{array} \right] = \left[ \begin{array}{cc} \sigma_{xx} & \sigma_{xy}\\ \sigma_{xy} & \sigma_{yy} \end{array} \right] $$ where $\langle\cdot\rangle$ denotes expected value.

Isodensity Surfaces

The level surfaces of the multivariate Gaussian distribution, $G({\bf x})$, consist of those points where $G({\bf x})$ has constant value:

\[ G({\bf x}) = \frac{1}{(2\pi)^{K/2} |{\bf C}|^{1/2}} e^{-\frac{1}{2}{\bf x}^{\;{\rm T}} {\bf C}^{-1} {\bf x}} = P \]

It follows that the level surfaces are ellipsoids: \[ {\bf x}^{\;{\rm T}} {\bf C}^{-1} {\bf x} = -2\ln \left[(2\pi)^{K/2} |{\bf C}|^{1/2} P\right] \]

Principal Axes of Gaussian Isodensity Ellipsoid

Level Surface: x^TC^-1x = 1

Axis 1 (w₁): a = 2.10 → λ₁ = 4.41

Axis 2 (w₂): b = 2.10 → λ₂ = 4.41

Axis 3 (w₃): c = 2.10 → λ₃ = 4.41

Principal Variances: λ_k = (semi-axis)²

Drag on canvas to rotate 3D view

Shape:

Principal Axes Theorem

The principal axes of the ellipsoids forming the level surfaces of the multivariate Gaussian distribution are given by the eigenvectors of its covariance matrix: \[ \lambda_k {\bf w}_k = {\bf C} {\bf w}_k \] where $|\lambda_1| > |\lambda_2| > \cdots |\lambda_K|$

Geometric ↔ Statistical Bridge:

Axis directions = eigenvectors ${\bf w}_k$ (orientation of the data cloud)
Semi-axis lengths = $\sqrt{\lambda_k}$ (standard deviation along that axis: $\sigma_k = \sqrt{\text{Var}}$)
Longest principal axis ${\bf w}_1$ ↔ direction of maximal variance!

TALKING POINTS FOR CLASS: 1. Where does this come from? (It doesn't come out of nowhere!): - In standard Cartesian geometry, an axis-aligned ellipse is: x^2/a^2 + y^2/b^2 = 1. - In matrix form, this is x^T D^{-1} x = 1, where the diagonal entries are a^2 and b^2. - When covariance C is not diagonal, the ellipse is simply rotated in space! 2. Spectral Theorem connection (from earlier in the lecture): - Because C is real and symmetric, C = W D W^T. - Rotating into the eigenvector basis W diagonalizes C and turns the tilted ellipsoid back into an axis-aligned ellipse! - Therefore, the axes of the tilted ellipse MUST align with the columns of W (the eigenvectors). 3. The Connection to Maximal Variance: - The level surface x^T C^{-1} x = 1 is the 1-standard-deviation (1-sigma) contour of the Gaussian cloud. - The semi-axis length along w_k is a = sqrt(lambda_k) = sigma_k. - The longest axis of that data cloud is where the data spreads the furthest--meaning MAXIMAL VARIANCE! - The shortest axis has the least spread (minimal variance). 4. Foreshadowing PCA Optimization (Slide 5.19): - Tell the students: "Right now we see this purely geometrically from the shape of the data ellipse. In a few slides, we will set up the optimization problem: max Var(w^T x) subject to ||w||=1. Calculus (Lagrange multipliers) will give us the EXACT SAME eigenvalue equation C w = lambda w! Geometry and optimization are two sides of the same coin."

Diagonalizing the Covariance Matrix

Because the covariance matrix, ${\bf C}$, is real, symmetric, and of full rank, it has $K$ orthogonal eigenvectors. It therefore can be diagonalized as follows: \[ {\bf C} = {\bf W}{\bf D}{\bf W}^{\rm T} \] where the $k$-th column of ${\bf W}$ is the eigenvector of ${\bf C}$ with the $k$-th largest eigenvalue and ${\bf D}$ is diagonal, with the corresponding eigenvalues on the diagonal: \[ D_{kk} = \lambda_k. \]

The KL Transform

We can represent the samples of the Gaussian distributed vector random variable, ${\bf x}$, in the basis formed by the eigenvectors, ${\bf w}_k$, of its covariance matrix, ${\bf C}$. This change of basis is termed the Karhunen-Loeve or KL Transform: \[ {\bf u} = {\bf W}^{\rm T} {\bf x} \] where ${\bf u} =\left[u, v \right]^{\rm T}$ is the representation of ${\bf x} = \left[x, y\right]^{\rm T}$ in the basis formed by the ${\bf w}_k$.

The KL Transform

Question What is the distribution of the ${\bf u}$?

Answer It is the multivariate Gaussian with covariance matrix, ${\bf D}$: \[ \hat{G}({\bf u}) = \frac{1}{(2\pi)^{K/2} |{\bf D}|^{1/2}} e^{-\frac{1}{2}{\bf u}^{\;{\rm T}} {\bf D}^{-1} {\bf u}}. \]

The Bivariate Case

\[ {\bf D} = {\bf W}^{\rm T}{\bf C}{\bf W} = \left[\begin{array}{cc} \sigma_{uu} & 0\\ 0 & \sigma_{vv} \end{array}\right] \]

Since ${\bf D}$ is diagonal, \[ |{\bf D}| = \sigma_{uu}\sigma_{vv} \]

and ${\bf D}^{-1}$ has an especially simple form: \[ {\bf D}^{-1} = \left[\begin{array}{cc} 1/\sigma_{uu} & 0\\ 0 & 1/\sigma_{vv} \end{array}\right] \]

The Bivariate Case (cont.)

The Gaussian distribution with covariance $\left[\begin{array}{cc} \sigma_{uu} & 0\\ 0 & \sigma_{vv} \end{array}\right]$ is:

\begin{eqnarray*} \hat{G}(u,v) & = & \frac{1}{2\pi \sqrt{\sigma_{uu}\sigma_{vv}}} e^{-\frac{1}{2}(\frac{u^2}{\sigma_{uu}} + \frac{v^2}{\sigma_{vv}})} \end{eqnarray*}

Observe that $\hat{G}$ is separable:

\[ \hat{G}(u,v) = \frac{1}{\sqrt{2\pi\sigma_{uu}}}e^{-\frac{u^2}{2\sigma_{uu}}} \frac{1}{\sqrt{2\pi\sigma_{vv}}}e^{-\frac{v^2}{2\sigma_{vv}}}. \]

Since the joint distribution of $u$ and $v$ can be expressed as the product of the distribution of $u$ and the distribution of $v$, we say that $u$ and $v$ are independent.
Knowing the value of $u$ tells you nothing about the value of $v$!

Two Views of PCA

Let $\vec{w}$ be an arbitrary candidate unit direction ($\|\vec{w}\| = 1$).
Centered data $\vec{x}_i \in \mathbb{R}^K$ with covariance ${\bf C} = \frac{1}{N}\sum_{i=1}^N \vec{x}_i \vec{x}_i^{\rm T}$.

1. Maximize Projected Variance

\[ \max_{\|\vec{w}\|=1} \frac{1}{N}\sum_{i=1}^N (\vec{w}^{\rm T}\vec{x}_i)^2 = \max_{\|\vec{w}\|=1} \vec{w}^{\rm T} {\bf C} \vec{w} \]

2. Minimize Reconstruction Error $d^2(\vec{w})$

\[ \min_{\|\vec{w}\|=1} d^2(\vec{w}) = \min_{\|\vec{w}\|=1} \frac{1}{N}\sum_{i=1}^N \|\vec{x}_i - (\vec{w}^{\rm T}\vec{x}_i)\vec{w}\|^2 \]

Dual Optimality: The Pythagorean Link

For sample $\vec{x}_i$, projection $\hat{\vec{x}}_i \perp$ error $\vec{e}_i$:
($\vec{w}^{\rm T}\vec{x}_i$ is coordinate along $\vec{w}$; $d_i = \|\vec{e}_i\|$) \[ \|\vec{x}_i\|^2 = (\vec{w}^{\rm T}\vec{x}_i)^2 + d_i^2 \]

Averaging over dataset of $N$ samples (${\bf C} = \frac{1}{N}\sum_{i=1}^N \vec{x}_i \vec{x}_i^{\rm T}$): \[ \underbrace{\text{Tr}({\bf C})}_{\text{Total Var (fixed)}} = \underbrace{\vec{w}^{\rm T}{\bf C}\vec{w}}_{\text{Projected Var}} + \underbrace{d^2(\vec{w})}_{\text{Reconstruction Error}} \implies d^2(\vec{w}) = \text{Tr}({\bf C}) - \vec{w}^{\rm T}{\bf C}\vec{w} \]

$\max \text{Projected Variance} \iff \min \text{Reconstruction Error}$

Why the Eigenvector?

Maximize variance $\vec{w}^{\rm T}{\bf C}\vec{w}$ subject to unit length $\|\vec{w}\|^2 = \vec{w}^{\rm T}\vec{w} = 1$:

Lagrange Multiplier: enforce unit-norm constraint with $\lambda$

\[ {\cal L}(\vec{w}, \lambda) = \vec{w}^{\rm T}{\bf C}\vec{w} - \lambda(\vec{w}^{\rm T}\vec{w} - 1) \]

Set gradient with respect to $\vec{w}$ to zero: \[ \nabla_{\vec{w}}{\cal L} = 2{\bf C}\vec{w} - 2\lambda\vec{w} = \vec{0} \quad \implies \quad {\bf C}\vec{w} = \lambda\vec{w} \]

Stationary points are precisely the eigenvectors of ${\bf C}$!

Multiply on left by $\vec{w}^{\rm T}$: \[ \vec{w}^{\rm T}{\bf C}\vec{w} = \lambda (\vec{w}^{\rm T}\vec{w}) = \lambda \]

Variance equals the eigenvalue: $\text{Var}(z) = \lambda$.
To maximize variance $\implies$ choose the largest eigenvalue $\lambda_1$ ($\vec{w}^* = \vec{w}_1$)!

PCA Dimensionality Reduction: Max Variance ↔ Min Error

Projected Var: 0.00 0.0%

Reconstruct Error: 0.00 0.0%

Var(z) + Error = Total Var: 0.00

● Drag green axis or slider to rotate projection

Axis θ: 0°

Show PC2 (⊥)

Dim k:

Data:

Take Home Points

OLS vs. PCA: OLS minimizes asymmetric vertical error $(y - \hat{y})^2$; PCA minimizes symmetric orthogonal distance $d_\perp^2$ (rotation-invariant).
Spectral Theorem: Real symmetric covariance factors as ${\bf C} = {\bf X} \Lambda {\bf X}^T = \sum \lambda_i \vec{x}_i \vec{x}_i^T$ into an orthogonal basis of rank-1 variance components.
Dual Optimality: Maximizing projected variance $\vec{w}^T{\bf C}\vec{w}$ $\iff$ minimizing reconstruction error $\sum d_\perp^2$ (Pythagorean conservation: $\text{Var} + \text{Error} = \text{Tr}({\bf C})$).
KL Transform: Eigenvector coordinates ${\bf u} = {\bf W}^T{\bf x}$ diagonalize covariance; for Gaussians, uncorrelated $\implies$ independent ($p(u,v) = p(u)p(v)$).
Optimal Compression: Truncating to top $k$ principal components captures maximal variance $\sum_{i=1}^k \lambda_i$ with minimal $\ell_2$ information loss.