Advanced Machine Learning

05: Linear models

Schedule (you are here )

#	date	topic	description
1	25-Aug-2025	Introduction
2	27-Aug-2025	Foundations of learning	Drop/Add
3	01-Sep-2025	Labor Day Holiday	Holiday
4	03-Sep-2025	Linear algebra (self-recap)	HW1
5	08-Sep-2025	PAC learnability
6	10-Sep-2025	Linear learning models
7	15-Sep-2025	Principal Component Analysis	Project ideas
8	17-Sep-2025	Curse of Dimensionality
9	22-Sep-2025	Bayesian Decision Theory	HW2, HW1 due
10	24-Sep-2025	Parameter estimation: MLE
11	29-Sep-2025	Parameter estimation: MAP & NB	finalize teams
12	01-Oct-2025	Logistic Regression
13	06-Oct-2025	Kernel Density Estimation
14	08-Oct-2025	Support Vector Machines	HW3, HW2 due
15	13-Oct-2025	* Midterm	Exam
16	15-Oct-2025	Matrix Factorization
17	20-Oct-2025	* Mid-point projects checkpoint	*
18	22-Oct-2025	k-means clustering

#	date	topic	description
19	27-Oct-2025	Expectation Maximization
20	29-Oct-2025	Stochastic Gradient Descent	HW4, HW3 due
21	03-Nov-2025	Automatic Differentiation
22	05-Nov-2025	Nonlinear embedding approaches
23	10-Nov-2025	Model comparison I
24	12-Nov-2025	Model comparison II	HW5, HW4 due
25	17-Nov-2025	Model Calibration
26	19-Nov-2025	Convolutional Neural Networks
27	24-Nov-2025	Thanksgiving Break	Holiday
28	26-Nov-2025	Thanksgiving Break	Holiday
29	01-Dec-2025	Word Embedding
30	03-Dec-2025	* Project Final Presentations	HW5 due, P
31	08-Dec-2025	Extra prep day	Classes End
32	10-Dec-2025	* Final Exam	Exam
34	17-Dec-2025	Project Reports	due
35	19-Dec-2025	Grades due 5 p.m.

Outline for the lecture

Linear decision boundary
Perceptron
Perceptron extensions
Non-separable case

Linear Decision Boundary

A Hyperplane

A Hyperplane

Controls:
W - Move red point (x)
E - Rotate normal vector (w)
R - Move hyperplane along normal
Right click - Orbit camera
Left click - Drag selected element
[Labels update automatically]

An example!

linearly separable, separating vector
The Iris flower data set or Fisher's Iris data set is a multivariate data set introduced by the British statistician, eugenicist, and biologist Ronald Fisher in his 1936 paper The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis.[1] It is sometimes called Anderson's Iris data set because Edgar Anderson collected the data to quantify the morphologic variation of Iris flowers of three related species.[2] Two of the three species were collected in the Gaspé Peninsula "all from the same pasture, and picked on the same day and measured at the same time by the same person with the same apparatus".[3] Fisher's paper was published in the journal, the Annals of Eugenics, creating controversy about the continued use of the Iris dataset for teaching statistical techniques today.
The data set consists of 50 samples from each of three species of Iris (Iris setosa, Iris virginica and Iris versicolor). Four features were measured from each sample: the length and the width of the sepals and petals, in centimeters. Based on the combination of these four features, Fisher developed a linear discriminant model to distinguish the species from each other.

Solution region

Example: linear separability

Perceptron

A Hyperplane

Ramon y Cajal

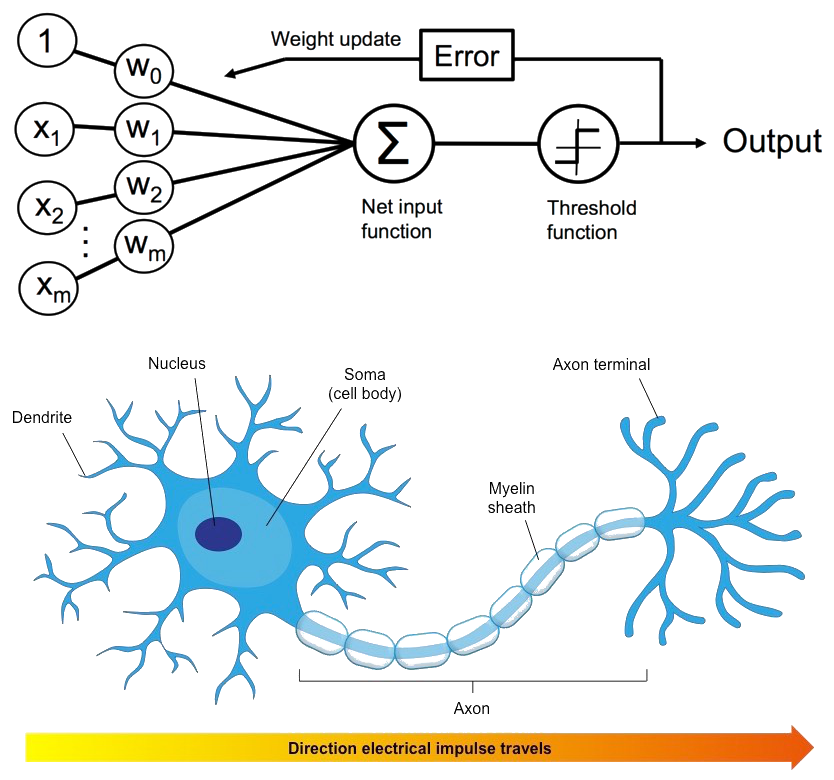
A Neuron

A Perceptron

Criterion (objective)

$$ J(\vec{w}) = -\sum_{\text{incorrect } i} l_i\vec{w}^Tx_i$$ $\vec{w}$ - parameters of our model (the perceptron)

Batch Perceptron

${\cal Y}$ is the set of samples misclassified by $\vec{w}$

Stochastic Perceptron

Stochastic Algorithm Convergence theorem

If the training samples are linearly separable then the sequence of weight vectors in line 4 of Algorithm 2 will terminate at a solution vector.

Proof

Let us show that for any solution $\widetilde{\vec{w}}$ the following holds: $$\|\vec{w}_{k+1} - \widetilde{\vec{w}}\| \le \|\vec{w}_{k} - \widetilde{\vec{w}}\| $$

Proof (1/3)

$\vec{w}_{k+1} = \vec{w}_k + l_k \vec{x}_k$

$l_k \widetilde{\vec{w}}^T\vec{x}_k > 0$

$\vec{w}_{k+1} - \alpha \widetilde{\vec{w}} = (\vec{w}_k - \alpha \widetilde{\vec{w}}) + l_k \vec{x}_k$

$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 = \|(\vec{w}_k - \alpha \widetilde{\vec{w}}) + l_k \vec{x}_k\|^2$

$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 = \|\vec{w}_k - \alpha \widetilde{\vec{w}}\|^2 + 2(\vec{w}_k - \alpha \widetilde{\vec{w}})^T\vec{x}_kl_k + \|l_k \vec{x}_k\|^2$

$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 = \|\vec{w}_k - \alpha \widetilde{\vec{w}}\|^2 + 2\vec{w}_k^T\vec{x}_kl_k - 2\alpha \widetilde{\vec{w}}^T\vec{x}_kl_k + \|l_k \vec{x}_k\|^2$

$\vec{w}_{k}^Tl_k \vec{x}_k \le 0$ since $\vec{x}_k$ was misclassified

$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 \le \|\vec{w}_k - \alpha \widetilde{\vec{w}}\|^2 - 2 \alpha \widetilde{\vec{w}}^Tl_k \vec{x}_k + \|l_k \vec{x}_k\|^2$

Proof (2/3)

$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 \le \|\vec{w}_k - \alpha \widetilde{\vec{w}}\|^2 - 2 \alpha \widetilde{\vec{w}}^Tl_k \vec{x}_k + \|l_k \vec{x}_k\|^2$

$\beta^2 = \underset{k}{\max}\|l_k \vec{x}_k\|^2 = \underset{k}{\max} \|\vec{x}_k\|^2$

$\gamma = \underset{k}{\min}\left[ \widetilde{\vec{w}}^T \vec{x}_kl_k\right] > 0$

$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 \le \|\vec{w}_k - \alpha \widetilde{\vec{w}}\|^2 - 2 \alpha \gamma + \beta^2$

$\alpha = \frac{\beta^2}{\gamma}$

$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 \le \|\vec{w}_k - \alpha \widetilde{\vec{w}}\|^2 - \beta^2$
The distance to solution is reduced by at least $\beta^2$ at each iteration.

Proof (3/3)

$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 \le \|\vec{w}_k - \alpha \widetilde{\vec{w}}\|^2 - \beta^2$
The distance to solution is reduced by at least $\beta^2$ at each iteration.

After $k$ iterations:
$\|\vec{w}_{k+1} - \alpha \widetilde{\vec{w}}\|^2 \le \|\vec{w}_1 - \alpha \widetilde{\vec{w}}\|^2 - k\beta^2$

The distance cannot become negative, so no more than $k_0$ iterations:
$k_0 = \frac{\|\vec{w}_1 - \alpha \widetilde{\vec{w}}\|^2}{\beta^2}$

Setting initial paramters to zero $\vec{w}_1 = \vec{0}$:
$k_0 = \frac{\alpha^2\|\widetilde{\vec{w}}\|^2}{\beta^2} = \frac{\beta^2\|\widetilde{\vec{w}}\|^2}{\gamma^2} = \frac{\underset{i}{\max} \|\vec{x}_i\|^2\|\widetilde{\vec{w}}\|^2}{\underset{i}{\min}\left[l_i\vec{x}_i^T\widetilde{\vec{w}}\right]}$

Perceptron Extensions

Margin

Perceptron with Margin

Perceptron Relaxation

Define the loss as $$ J_r(\vec{w}) = \frac{1}{2} \underset{\text{incorrect}}{\sum} \frac{(\vec{w}^T\vec{x}l - b)^2}{\|l\vec{x}\|^2} $$

Then the gradient is $$ \nabla_{\vec{w}} J_r = \underset{\text{incorrect}}{\sum} \frac{\vec{w}^T\vec{x}l - b}{\|l\vec{x}\|^2}\vec{x}l $$

Perceptron Relaxation

Perceptron Relaxation: interpretation

$$ r(k) = \frac{b - \vec{w}_k^T\vec{x}_kl_k}{\|\vec{x}_kl_k\|} $$

Non-separable case

Separable example

Multiple restarts

Non-separable example

AI winter

What we usually encounter

Criterion (objective/loss)

$$ J(\vec{w}) = -\sum_{\text{incorrect } i} l_i\vec{w}^T\vec{x}_i$$ $\vec{w}$ - parameters of our model (the perceptron) $$ J_{\text{MSE}}(\vec{w}) = \frac{1}{2}\sum_{\forall i} (\vec{w}^T\vec{x}_i - b_i)^2$$ $$ \nabla_{\vec{w}} J_{\text{MSE}} = \sum_{\forall i} (\vec{w}^T\vec{x}_i - b_i)\vec{x}_i$$

Least Mean Squares

Least Mean Squares