Advanced Machine Learning

02: foundations

Schedule (you are here )

#	date	topic	description
1	25-Aug-2025	Introduction
2	27-Aug-2025	Foundations of learning	Drop/Add
3	01-Sep-2025	Labor Day Holiday	Holiday
4	03-Sep-2025	Linear algebra (self-recap)	HW1
5	08-Sep-2025	PAC learnability
6	10-Sep-2025	Linear learning models
7	15-Sep-2025	Principal Component Analysis	Project ideas
8	17-Sep-2025	Curse of Dimensionality
9	22-Sep-2025	Bayesian Decision Theory	HW2, HW1 due
10	24-Sep-2025	Parameter estimation: MLE
11	29-Sep-2025	Parameter estimation: MAP & NB	finalize teams
12	01-Oct-2025	Logistic Regression
13	06-Oct-2025	Kernel Density Estimation
14	08-Oct-2025	Support Vector Machines	HW3, HW2 due
15	13-Oct-2025	* Midterm	Exam
16	15-Oct-2025	Matrix Factorization
17	20-Oct-2025	* Mid-point projects checkpoint	*
18	22-Oct-2025	k-means clustering

#	date	topic	description
19	27-Oct-2025	Expectation Maximization
20	29-Oct-2025	Stochastic Gradient Descent	HW4, HW3 due
21	03-Nov-2025	Automatic Differentiation
22	05-Nov-2025	Nonlinear embedding approaches
23	10-Nov-2025	Model comparison I
24	12-Nov-2025	Model comparison II	HW5, HW4 due
25	17-Nov-2025	Model Calibration
26	19-Nov-2025	Convolutional Neural Networks
27	24-Nov-2025	Thanksgiving Break	Holiday
28	26-Nov-2025	Thanksgiving Break	Holiday
29	01-Dec-2025	Word Embedding
30	03-Dec-2025	* Project Final Presentations	HW5 due, P
31	08-Dec-2025	Extra prep day	Classes End
32	10-Dec-2025	* Final Exam	Exam
34	17-Dec-2025	Project Reports	due
35	19-Dec-2025	Grades due 5 p.m.

Outline for the lecture

Problem statement
Inductive bias
Bound for the probability of error

Problem Statement

Imagine you have just arrived in some small Pacific island. You soon find out that papayas are a significant ingredient in the local diet. However, you have never before tasted papayas. You have to learn how to predict whether a papaya you see in the market is tasty or not. First, you need to decide which features of a papaya your prediction should be based on. On the basis of your previous experience with other fruits, you decide to use two features: the papaya’s color, ranging from dark green, through orange and red to dark brown, and the papaya’s softness, ranging from rock hard to mushy. Your input for figuring out your prediction rule is a sample of papayas that you have examined for color and softness and then tasted and found out whether they were tasty or not. Let us analyze this task as a demonstration of the considerations involved in learning problems.
from Shalev-Shwartz S, Ben-David S. ``Understanding machine learning: From theory to algorithms.'' Cambridge university press; 2014

setup

Domain Set ${\cal X}$ (all papayas)
Label set ${\cal Y}$
Training data
The learner's output (ὑπόθεσις)
A (simple) data-generation model
- $\cal{D}$ - distribution of papayas
- $f: \cal{X} \rightarrow \cal{Y}$ - true labeling function
- $y_i = f(x_i) \forall i$

Measure of success: true loss

for $A \subset \cal{X}$, ${\cal D}(A)$ is how likely to observe $x\in A$

$A$ is an event expressed as $\pi:{\cal X}\rightarrow \{0,1\}$

$A = \{x\in {\cal X}: \pi(x) = 1\}$

then $\mathbb{P}_{x \sim {\cal D}}[\pi(x)]$ expresses ${\cal D}(A)$

$L_{({\cal D},f)}(h) \stackrel{\text{def}}{=}\mathbb{P}_{x \sim {\cal D}}[h(x) \ne f(x)]$

generalization error, the risk, the true error of $h$, or loss!

Measure of success: empirical loss

Training set $S\sim {\cal D}$
Expected predictor $h_s: \cal{X} \rightarrow \cal{Y}$
Find $h_S$ that minimizes a loss with respect to unknown ${\cal D}$ and $f$

$L_{S}(h) \stackrel{\text{def}}{=} \frac{\mid\{i\in\{1,\dots,m\}:h(x_i) \ne y_i\}\mid}{m}$

Empirical Risk Minimization

What can go wrong?

overfitting

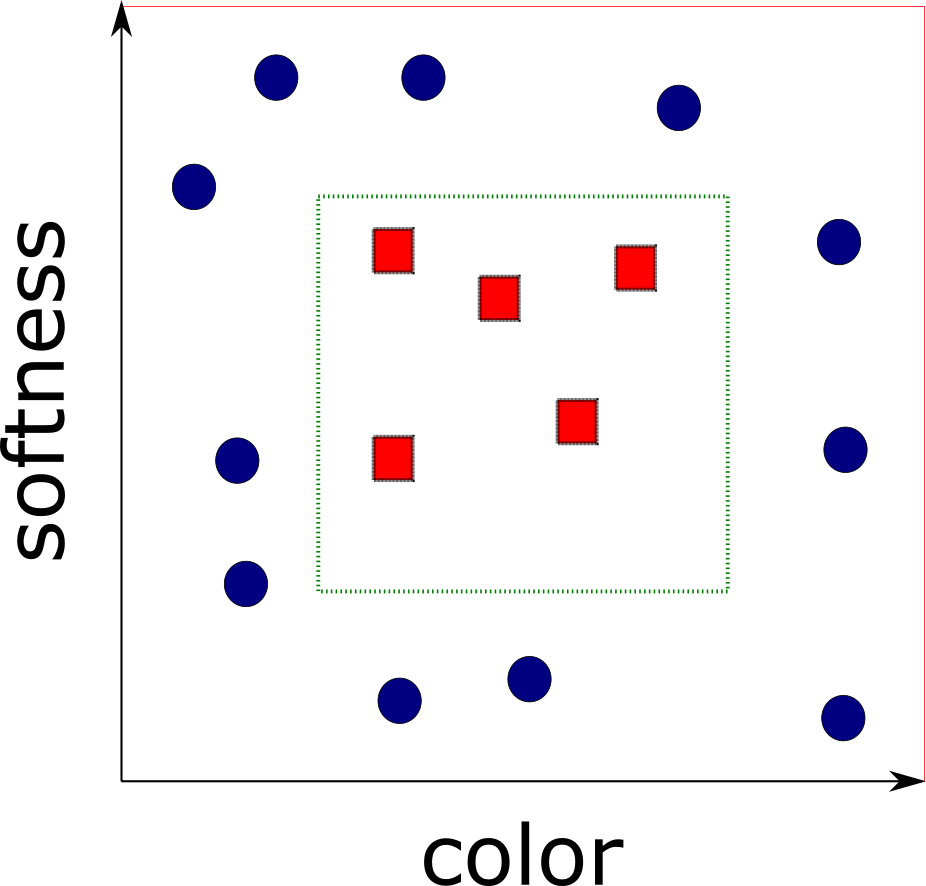
$h_S(x) = \begin{cases} y_i & \text{if } \exists i \in \{1,\dots,m\} s.t. x_i=x\\ 0 & \text{otherwise} \end{cases} $

$L_{S}(h_S) = 0$ yet $L_{\cal D}(h_S) = 1/2$

Inductive bias

Bait shyness

Pigeon superstition

B. F. Skinner conditions a pigeon

What about rat superstition and conditioning?

What can we do in our case?

Search over a restricted search space.
- Choose hypothesis class ${\cal H}$ in advance
- $\forall h\in {\cal H}, h: \cal{X} \rightarrow \cal{Y}$

Inductive bias

$\text{ERM}_{\cal H}(S) \stackrel{\text{def}}{=} \underset{h\in{\cal H}}{\argmin}L_S(h)$
bias the learner to a particular set of predictors

Other inductive biasi

Maximum conditional independence
cast in a Bayesian framework, try to maximize conditional independence (Naive Bayes)
Minimum cross-validation error
Maximum margin
Minimum description length
Minimum features
Nearest neighbors

Finite Hypothesis Classes

$h_S \in \underset{h\in{\cal H}}{\argmin}L_S(h)$

Bound the probability of error

Assumptions

The Realizability Assumption: There exists $h^* \in {\cal H}$ s.t. $L_{{\cal D}, f}(h^*)=0$. This implies: with probability 1 over random samples $S\sim {\cal D}$ labeled by $f$, we have $L_S(h^*)=0$

The i.i.d. Assumption: Samples in the training set are independent and identically distributed. Denoted as $S\sim {\cal D}^m$

Confidence and accuracy

The risk $L_{({\cal D},f)}(h_S)$ depends on the randomly picked training set $S$. We say, the risk is a random variable.

Some training sets $S$ can be really bad! Denote the probability of getting a nonrepresentative sample by $\delta$

Let's call $(1-\delta)$ - confidence parameter

Can't hope to always have perfect loss $L_{({\cal D}, f)}=0$. Let's introduce the accuracy parameter $\epsilon$.

Failure is when $L_{({\cal D}, f)}>\epsilon$
Success is when $L_{({\cal D}, f)}\le \epsilon$

What is the probability of a bad sample that fails the learner?

$S\mid_x = (x_1, x_2, \dots, x_m)$ - instances of the training set

We want to upperbound ${\cal D}^m(\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon\})$

The set of "bad" hypotheses ${\cal H}_B = \{h\in {\cal H} : L_{({\cal D}, f)}(h) > \epsilon\})$

Set of misleading samples $M = \{S\mid_x : \exists h \in {\cal H}_B, L_S(h)=0\}$

But remember our assumption?

The Realizability Assumption: There exists $h^* \in {\cal H} s.t. L_{{\cal D}, f}(h^*)=0$. This implies: with probability 1 over random samples $S\sim {\cal D}$ labeled by $f$, we have $L_S(h^*)=0$

Means $L_S(h_S) = 0$, where $h_S \in \underset{h\in{\cal H}}{\argmin}L_S(h)$.

Hence $L_{({\cal D}, f)}(h_S) > \epsilon$ can only happen if for some $h\in {\cal H}_B$, $L_S(h)=0$

follows $\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon \} \subseteq M$

We want to upperbound ${\cal D}^m(\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon\})$

$\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon \} \subseteq M$

rewrite set of misleading samples $M = \{S\mid_x : \exists h \in {\cal H}_B, L_S(h)=0\}$

as $M = \underset{h\in {\cal H}_B}\bigcup \{S\mid_x : L_{S}(h) = 0 \}$

${\cal D}^m(\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon\}) \le {\cal D}^m(M)$

${\cal D}^m(M) = {\cal D}^m(\underset{h\in {\cal H}_B}\bigcup \{S\mid_x : L_{S}(h) = 0 \})$

Confidence and accuracy

Union Bound: For any two sets $A$, $B$ and a distribution $\cal D$ we have ${\cal D}(A\cup B) \le {\cal D}(A) + {\cal D}(B)$

hence
\begin{align} {\cal D}^m(\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon\}) & \le \\ {\cal D}^m(\underset{h\in {\cal H}_B}\bigcup \{S\mid_x : L_{S}(h) = 0 \}) & \le \\ \sum_{h\in {\cal H}_B}{\cal D}^m(\{S\mid_x : L_{S}(h) = 0 \}) \end{align}

let's put a bound on each summand separately

Confidence and accuracy

Let's put a bound on each summand separately
${\cal D}^m(\{S\mid_x : L_{S}(h) = 0 \}) = $
${\cal D}^m(\{S\mid_x : \forall i, h(x_i) = f(x_i) \})$
$= \prod_{i=1}^m {\cal D}(\{x_i: h(x_i) = f(x_i)\})$

remember we are only considering bad hypotheses
$h\in{\cal H}_B = \{h\in {\cal H} : L_{({\cal D}, f)}(h) > \epsilon\}$

${\cal D}(\{x_i: h(x_i) = f(x_i)\}) = 1 - L_{({\cal D}, f)}(h) \le 1-\epsilon$

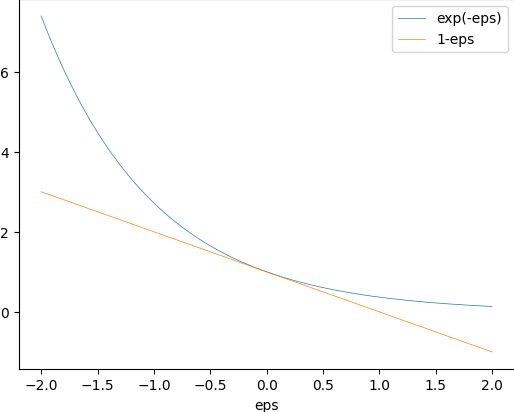
using $1-\epsilon \le e^{-\epsilon}$
${\cal D}^m(\{S\mid_x : L_{S}(h) = 0 \}) \le (1-\epsilon)^m \le e^{-\epsilon m}$

the final bound

${\cal D}^m(\{S\mid_x : L_{S}(h) = 0 \}) \le e^{-\epsilon m}$
${\cal D}^m(\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon\}) \le \sum_{h\in {\cal H}_B}{\cal D}^m(\{S\mid_x : L_{S}(h) = 0 \})$
$\sum_{h\in {\cal H}_B}{\cal D}^m(\{S\mid_x : L_{S}(h) = 0 \}) \le \mbox{ ?}$
$\sum_{h\in {\cal H}_B}{\cal D}^m(\{S\mid_x : L_{S}(h) = 0 \}) \le |{\cal H}_B|e^{-\epsilon m}$
$|{\cal H}_B|e^{-\epsilon m}\le |{\cal H}|e^{-\epsilon m}$
${\cal D}^m(\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon\}) \le \sum_{h\in {\cal H}_B}{\cal D}^m(\{S\mid_x : L_{S}(h) = 0 \})$
${\cal D}^m(\{S\mid_x : L_{({\cal D}, f)}(h_S) > \epsilon\}) \le |{\cal H}|e^{-\epsilon m}$